区块链中的数学 - 参与者 < 门限值t的密钥更新Amir Herzberg方案
- blocksight
- 发布于 2020-12-06 18:30
- 阅读 6216
本文介绍参与者少于门限值t时的方案,实质上是通过提高c的值来改变门限值。 需要说明的是后m个节点虽然也参与计算了,但不是和前k节点一样(生成秘密随机数,计算准备多项式),属于被动参与,不会影响最终结果。
写在前面
上一节讲了动态密钥分享方案,攻击者必须在一个时间段内,获得门限值t (threshold)个密钥分片,由于时间限制,提高攻击难度,使得旧密钥可以安全删除。只要参与动态更新的节点数 >= 门限值t (threshold).
本文说下如果参与密钥分片更新的参与者少于门限值 t 时,该如何处理?
理解本文的基础是前一篇,空中楼台终难稳固,如果不了解,建议先搞懂背景知识!
Amir Herzberg改进方案
本文的符号含义,未提及的与上文一致!
假设参与密钥分片更新的节点数为k, k < t, 参与者记为$P_i,i \in [1,2,...,k]$ 新的密钥分片更新如下:
- 每个参与者$P_i$都随机选择一个$x_i \in Z_q^*$, 公开$g^{x_i}$给其他参与者,
- $P_i$检查$x_i$值与其他参与者值均不同,继续执行,否则重新选择。 令 $Bi(m)=\prod {j-1}^k,j\neq i \frac{m-j}{i-j}$, 其中m 取值k+1,k+2,...,n 再随机选择$\lambda{i1},\lambda{i2},...,\lambda{ik},\lambda{ij}\in Z_q^* $,且两两不等. 使得:$x_iBi(m)=\lambda{i1}^{(m)}+\lambda{i2}^{(m)}+...+\lambda{ik}^{(m)}$ 将$\lambda_{ij}^{(m)}$发送给其他参与者$P_i,j\in [1,k]$
-
$Pj$收到其他参与者发来的$\lambda{ij}^{(m)}$,执行计算$$ \lambdaj^{(m)}=\sum{i=1}^k \lambda_{ij}^{(m)} $$
发送给其余节点$P_m,m \in [k+1,n]$
$P_i$密钥分片更新为:$s_i’=s_i+x_i*i^{t-k}$
到此,k个参与密钥分片即子密钥更新操作完成,接下来是剩余n - k节点自行计算更新子密钥。
- $P_m, m\in[k+1,n]$计算: $xm= \sum{j=1}^k \lambda_j^{(m)}$ $s_m'=s_m+x_m*m^{t-k}$
原理分析
步骤1是每个节点生成一个秘密随机数,使用幂的方式公开(当然,具体实现可以是多种形式)。 步骤2利用公开的幂来比较自己生成的随机数是否与别人重复,要确保唯一, 然后利用拉格朗日插值法构造多项式元素。 步骤3 每个参与交互更新的节点准备多项式元素,供步骤4使用
步骤4的节点是没有参与前三步骤的节点,也就是说不在k之内。节点单独计算,没有任何交互。
总结来说,该方案的原理是利用插值法构造一个k-1次多项式,有k个点$(i,x_i), i=1,2,...,k$ , 多项式$h(x) = b_0+b1x+...+b{k-1}x^{k-1},x_i=h(i)$, 可得$x_m=h(m),m\in [k+1,n]$
证明简单如下式:
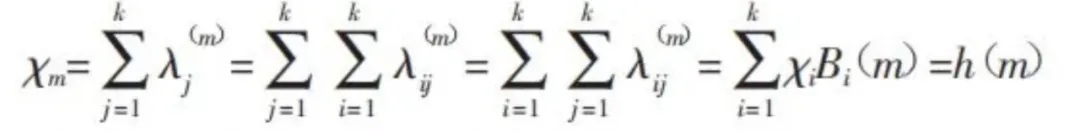
存储的子密钥更新是通过多项式$p(x) = h(x)x^c,c = t - k$, 将原来多项式变更为 $f'(x)=f(x)+p(x)$ 参与者$P_i$存储的密钥分片更新为: $s'_i=f(i)+p(i)=s_i+x_ii^c=s_i+h(i)i^c$
对比上一篇,可以发现当c = 0 即k = t 退化成经典的Amir Herzberg密钥更新方案。
如果对以上多项式构造过程不明白,说明拉格朗日插值知识有所欠缺,建议看下该方法涉及文章
小结
本文介绍参与者少于门限值t时的方案,实质上是通过提高c的值来改变门限值。 需要说明的是后m个节点虽然也参与计算了,但不是和前k节点一样(生成秘密随机数,计算准备多项式),属于被动参与,不会影响最终结果。
密钥分享是密码学中一个细分方向,除了最近几篇介绍的方法方案外,还有其他的,如基于中国剩余定理的方案,动态添加或者删除参与者的方案,一次分享多个密钥(秘密)的方案等。
本系列文章聚焦区块链领域,所以暂时不再进行更深入介绍。
下一篇将继续介绍区块链中应用的BLS签名以及阈值签名实现相关!
欢迎关注公众号:blocksight
相关阅读:
区块链中的数学 - Amir Herzberg动态密钥共享 Amir Herzberg动态密钥分享方案
区块链中的数学 - Feldman的可验证的密钥分享 Feldman可验证密钥分享方案
区块链中的数学 - Shamir密钥分享 Shamir原始的密钥分享方案
区块链中的数学 - 比特币使用的多签方式 比特币多签和Schnorr聚合签名
区块链中的数学 - 随机数和伪签名 随机数与伪签名构造
区块链中的数学 - EdDSA签名机制 EdDSA的发展及优点
区块链中的数学 - Ed25519签名 Ed25519签名
区块链中的数学-ElGamal算法 ElGamal算法签名及验证&实例演练
区块链中的数学-VRF基于ECC公钥体制的证明验证过程 基于椭圆曲线的VRF证明验证过程
Schorr签名与椭圆曲线 Schorr签名与椭圆曲线
区块链中的数学-Uniwap自动化做市商核心算法解析 Uniwap核心算法解析(中)
- Uniswap v3 数学洞察系列翻译 —— 第六部分 共 6 部分 3892 浏览
- Uniswap v3 数学洞察系列翻译 —— 第五部分 共 6 部分 4017 浏览
- Uniswap v3 数学洞察系列翻译 —— 第四部分 共 6 部分 4439 浏览
- Uniswap v3 数学洞察系列翻译 —— 第三部分 共 6 部分 5298 浏览
- Uniswap v3 数学洞察系列翻译 —— 第二部分 共 6 部分 3414 浏览
- Uniswap v3 数学洞察系列翻译 —— 第一部分 共 6 部分 3991 浏览
- stark数学基础和翻译名词 3308 浏览
- 区块链中的数学--PLookup 7339 浏览
- 区块链中的数学 -- MultiSet check& Schwartz–Zippel lemma 6845 浏览
- 区块链中的数学 - 环签名(ring signature) 16185 浏览
- 区块链中的数学 -盲签名(Blind Signature) 13944 浏览
- 区块链中的数学 - sigma协议OR Proof&签名 7877 浏览

