零知识证明之书

RareSkills
发布于 2024-09-01 13:36
阅读 38

《The RareSkills Book of Zero Knowledge》是一本面向程序员的零知识证明教程，内容涵盖从基础数学到实际编码实现，旨在帮助程序员深入理解零知识证明，尤其是Groth16算法。

## RareSkills 零知识证明之书

这是最友好的零知识证明教程

本书的构建指导思想很简单：令人瞩目的清晰度

![](https://img.learnblockchain.cn/2025/02/27/book-zero-knowledge-proofs.png.webp)

## 目录

### 模块 1   零知识证明的基础数学

第 1 章

[P vs NP 及其在零知识证明中的应用](https://learnblockchain.cn/article/9569)

第 2 章

[算术电路](https://learnblockchain.cn/article/11317)

第 3 章

[有限域与模运算](https://learnblockchain.cn/article/11315)

第 4 章

[集合论](https://learnblockchain.cn/article/9540)

第 5 章

[抽象代数](https://learnblockchain.cn/article/11382)

第 6 章

[群论](https://learnblockchain.cn/article/11320)

第 7 章

[同态](https://learnblockchain.cn/article/11385)

第 8 章

[椭圆曲线加法](https://learnblockchain.cn/article/11323)

第 9 章

[有限域上的椭圆曲线](https://learnblockchain.cn/article/11316)

### 模块 2 ZK-SNARKS 第 1 部分 (Groth16)

第 1 章

[双线性配对](https://learnblockchain.cn/article/11321)

第 2 章

[等级 1 约束系统](https://learnblockchain.cn/article/11313)

第 3 章

[带有 R1CS 的零知识证明](https://learnblockchain.cn/article/11355)

第 4 章

[使用 Python 进行拉格朗日插值](https://learnblockchain.cn/article/11371/)

第 5 章

[施瓦茨-齐佩尔引理](https://learnblockchain.cn/article/11356)

第 6 章

[二次算术程序](https://learnblockchain.cn/article/11314)

第 7 章

[Python 中的 R1CS 到 QAP](https://learnblockchain.cn/article/11318)

第 8 章

[可信设置](https://learnblockchain.cn/article/11357)

第 9 章

[在可信设置上评估 QAP](https://learnblockchain.cn/article/11327)

第 10 章

[Groth16 解释](https://learnblockchain.cn/article/11324)

### 模块 3  Bulletproofs：用于内积论证的 ZKP

第 1 章

[Bulletproofs 解释](https://learnblockchain.cn/article/11359)

第 2 章

[佩德森承诺](https://learnblockchain.cn/article/11358)

第 3 章

[佩德森多项式承诺](https://learnblockchain.cn/article/11365)

第 4 章

[零知识乘法（无配对）](https://learnblockchain.cn/article/11370)

第 5 章

[内积论证](https://learnblockchain.cn/article/11362)

第 6 章

[使用外积计算内积](https://learnblockchain.cn/article/11364)

第 7 章

[内积的对数大小证明](https://learnblockchain.cn/article/11363)

第 8 章

[Bulletproof ZKP 算法](https://learnblockchain.cn/article/11359p)

第 9 章

[内积代数](https://learnblockchain.cn/article/11361)

第 10 章

[零知识的随机线性组合](https://learnblockchain.cn/article/11368)

第 11 章

[范围证明](https://learnblockchain.cn/article/11369)

## 额外的零知识证明材料

[ Tornado Cash 是如何运作的](https://learnblockchain.cn/article/11263) 
[Circom 中的零知识难题](https://learnblockchain.cn/article/11379) 
[Noir 和 NextJS](https://learnblockchain.cn/article/11353) 
[Noir 中的零知识难题](https://github.com/RareSkills/noir-puzzles) 
[零知识编程语言](https://learnblockchain.cn/article/11352)

### 关于本书

本书并不是零知识主题的集合。它是一个有观点的子集，关于你需要了解的内容，以便从头开始编写一个实用的零知识证明者和验证者（ZK-SNARK）。

概念性理解和具体理解之间存在区别。大多数聪明人阅读教程后能够获得概念性理解，但他们与实际使用这些知识之间仍有很大差距。

对于数学家而言，具体理解发生在他们写出证明的时候。对于程序员而言，具体理解发生在他们写出功能代码时。

RareSkills 的零知识书籍非常适合想要获得具体理解的程序员。我们的书充满了代码片段，并展示了实际加密库的使用。我们使用数学符号，但以一种将其翻译为源代码仅需小步骤的方式书写它。

Groth16 是玛莎现金（以及许多其他应用）用于在链上实现零知识证明的算法。我们认为它是你学习旅程的最佳起点，而我们的书是完全理解该算法的最直接途径。

## 学习零知识的现实期望

学习零知识证明是一回事（很少有人成功做到），成功帮助其他工程师学习这个主题又是另一回事。很少有机构具备这种资格，我们很自豪 RareSkills 是其中之一。以下是我们所学到的内容：

** 1\. 如果你之前没有完成线性代数课程，你可能没有足够的数学成熟度来真正掌握这个主题**

就像如果你连计算器都无法编写，根本无法理解“面向对象编程”一样，没有足够的数学基础也无法理解零知识证明。然而，需要的数学远没有人们认为的那么先进。“抽象代数”听起来吓人，但其实并不。我们的书介绍了你所需的所有抽象代数。“有限域”可能听起来很高级，但其实并不是。

但是，轻数学的零知识证明介绍是自相矛盾的。零知识证明从根本上是数学性的。

线性代数的专业知识并非必需，但你应该理解什么是内积，矩阵乘法是如何工作的，以及什么是线性相关。如果你理解矩阵的行列式与两个方阵的乘积之间的关系，那就更好，但这并不是必要的。

**2\. 数学符号是高效的，你应该能够合理地使用它**

如果你无法弄清楚为什么

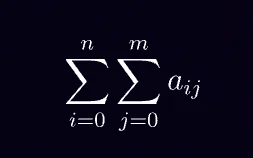
![](https://img.learnblockchain.cn/2025/02/27/cf9bcdc4ed81bbf640a1985ed0523d81.png.webp)

基本上是一个双重 for 循环，那么理解零知识证明将是一个挑战

我们本可以把它写成

![](https://img.learnblockchain.cn/2025/02/27/ece92fb7fc0ad818dfb2c1e5941ed773.png.webp)

但注意，这是一种更啰嗦的表达方式。我们的零知识教程用英语解释了符号，但你需要能够阅读它，即使这意味着用笔和纸逐步抄写公式。

流利阅读数学符号并不是一个要求，但你应该能够没有过多努力地翻译它。

**3\. 零知识中有大量简单但不熟悉的话题**

大多数程序员理解多项式，但你是否曾坐下来思考过为什么一个乘积多项式的根是构成该乘积的两个多项式根的并集？这条信息在大多数情况下是无用的——除非在研究零知识证明时。在零知识证明中，简单但“无用”的数学突然变得有用。因为你可能没有锻炼依赖于这种数学的大脑部分，所以会觉得更加困难。

**4\. 学习零知识证明不可能低于 80 小时的努力，这是最好的情况**

虽然本书分为 12 章，但在 12 天内掌握材料是非常不现实的。每个主题对于大多数程序员来说都是陌生的，每个主题的“浸入”期大约是一个星期，假设你正在积极思考该概念并编写代码来测试你的知识。

我们认为，对于具有足够数学背景的工程师而言，12-18 周的自律自学是现实的。

你需要亲身参与这个主题，以获得直观感受——而我们的书提供了很多如何做到这一点的建议。就像你不能仅通过阅读一本书或观看视频来学习编码一样，没有实际处理相关数学，你无法学习零知识证明。

如果你刚完成数学本科课程，并且有幸上过椭圆曲线的课程，这本书对你来说将会很轻松。实际上，我们期望不到 5% 的读者符合该条件。

#### 这本书是严格务实的

我们的目标是让你能够从零开始构建证明者和验证者。任何不直接有助于实现这一目标的知识都被跳过。有些在其他地方广泛讨论的主题在本书中被省略或延后讨论。例如，我们没有直接讨论完整性和正确性的定义，也没有解释提取器和模拟器是什么（尽管我们广泛讨论了与此相关的证明伪造）。

更令人惊讶的是，交互式 oracle 证明和 Fiat-Shamir 转换没有在早期讨论，我们没有直接解释多项式承诺方案。你可能在其他资源中看到过这些内容的详细讨论，但我们故意省略了它们。为什么？

对于来自编程背景的 zk 初学者来说，这些主题在理论上是越界的。

这并不意味着我们忽视理论——本书的前五章都是我们认为重要的数学。我们对哪些理论直接影响实践以及哪些理论仅在长远内有影响非常有主见。

本书（和训练营）的目标是帮助你从头开始构建证明者和验证者。尽管上述主题显然对任何想要成为专家的人重要，但不应该太早学习。类似地，我们也没有包括关于零知识证明的常见类比，如阿里巴巴洞穴或沃尔顿在哪里，因为这些并不能帮助你更接近实际编写代码的目标。

#### 我们的训练营是值得的

我们非常有信心，与你一起学习 zk 证明能够帮助你节省至少 50 小时的学习时间。如果你具备理解 zk 证明的技术背景和动机，那么你的时间可能相当宝贵，为什么不充分利用呢？

不要觉得自己太酷而不上学。大型公司的协议负责人和工程管理层都参加了这个课程，所以你会身处好公司。这并不是因为他们智商不够去理解以上的材料并学习，而是因为他们时间的价值在每小时数百美元，因此节省（至少）50 小时的时间是值得花钱的。

我们并不是说你不能独立学习 zk 证明，这确实是可能的，我们认为 RareSkills 的零知识书籍是做到这一点的最佳方法。不过，如果你与我们的社区和讲师一起学习，这个过程会快得多。

查看[ZK 训练营](https://learnblockchain.cn/column/117)

#### 结果

我们的一名学生记录了他从头开始实现 Groth16 零知识证明协议的证明者和验证者的旅程。

你可以在这里查看他的 [五部分写作](https://learnblockchain.cn/article/11383)。你还可以看到 [Optimizoor](https://twitter.com/optimizoor) （向量派）的 [实现](https://gist.github.com/Vectorized/dc66341e87fe8897a139c446e7e3316b)。

#### 其他资源呢？

我们并不是第一个尝试解释这个困难主题的人。这里有其他我们知道的高质量资源，有时，从多个角度看待主题是有帮助的。

- [electriccoin 教程](https://electriccoin.co/blog/snark-explain/)
- [zk-SNARK 是如何工作的以及为什么](https://arxiv.org/abs/1906.07221)，（中等版）
- [零知识博客教程](https://zeroknowledgeblog.com/index.php/the-pinocchio-protocol)
- [Least Authority 的月球数学手册](https://leastauthority.com/community-matters/moonmath-manual/)
- [ZK 学习](https://zk-learning.org/) 这是从学术角度教授，因此相当理论化。然而，如果你想深入研究研究文献，这是一个很好的起点。在使用此资料之前，最好已经修过其他的加密课程和抽象代数的课程。

>- 原文链接： [rareskills.io/zk-book...](https://www.rareskills.io/zk-book)
>- 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～

RareSkills 零知识证明之书

这是最友好的零知识证明教程

本书的构建指导思想很简单：令人瞩目的清晰度

额外的零知识证明材料

Tornado Cash 是如何运作的 Circom 中的零知识难题 Noir 和 NextJS Noir 中的零知识难题零知识编程语言

关于本书

本书并不是零知识主题的集合。它是一个有观点的子集，关于你需要了解的内容，以便从头开始编写一个实用的零知识证明者和验证者（ZK-SNARK）。

概念性理解和具体理解之间存在区别。大多数聪明人阅读教程后能够获得概念性理解，但他们与实际使用这些知识之间仍有很大差距。

对于数学家而言，具体理解发生在他们写出证明的时候。对于程序员而言，具体理解发生在他们写出功能代码时。

学习零知识的现实期望

1. 如果你之前没有完成线性代数课程，你可能没有足够的数学成熟度来真正掌握这个主题

但是，轻数学的零知识证明介绍是自相矛盾的。零知识证明从根本上是数学性的。

2. 数学符号是高效的，你应该能够合理地使用它

如果你无法弄清楚为什么

基本上是一个双重 for 循环，那么理解零知识证明将是一个挑战

我们本可以把它写成

但注意，这是一种更啰嗦的表达方式。我们的零知识教程用英语解释了符号，但你需要能够阅读它，即使这意味着用笔和纸逐步抄写公式。

流利阅读数学符号并不是一个要求，但你应该能够没有过多努力地翻译它。

3. 零知识中有大量简单但不熟悉的话题

4. 学习零知识证明不可能低于 80 小时的努力，这是最好的情况

我们认为，对于具有足够数学背景的工程师而言，12-18 周的自律自学是现实的。

如果你刚完成数学本科课程，并且有幸上过椭圆曲线的课程，这本书对你来说将会很轻松。实际上，我们期望不到 5% 的读者符合该条件。

这本书是严格务实的

对于来自编程背景的 zk 初学者来说，这些主题在理论上是越界的。

这并不意味着我们忽视理论——本书的前五章都是我们认为重要的数学。我们对哪些理论直接影响实践以及哪些理论仅在长远内有影响非常有主见。

我们的训练营是值得的

查看ZK 训练营

结果

我们的一名学生记录了他从头开始实现 Groth16 零知识证明协议的证明者和验证者的旅程。

你可以在这里查看他的五部分写作。你还可以看到 Optimizoor （向量派）的实现。

其他资源呢？

我们并不是第一个尝试解释这个困难主题的人。这里有其他我们知道的高质量资源，有时，从多个角度看待主题是有帮助的。

electriccoin 教程
zk-SNARK 是如何工作的以及为什么，（中等版）
零知识博客教程
Least Authority 的月球数学手册
ZK 学习这是从学术角度教授，因此相当理论化。然而，如果你想深入研究研究文献，这是一个很好的起点。在使用此资料之前，最好已经修过其他的加密课程和抽象代数的课程。

原文链接： rareskills.io/zk-book...

登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～

本文参与登链社区写作激励计划，好文好收益，欢迎正在阅读的你也加入。

零知识证明之书

RareSkills 零知识证明之书

目录

模块 1 零知识证明的基础数学

模块 2 ZK-SNARKS 第 1 部分 (Groth16)

模块 3 Bulletproofs：用于内积论证的 ZKP

额外的零知识证明材料

关于本书

学习零知识的现实期望

这本书是严格务实的

我们的训练营是值得的

结果

其他资源呢？

0 条评论

文章目录