区块链中的数学 - 爱德华曲线方程
- blocksight
- 更新于 2020-10-21 13:01
- 阅读 7173
本文简要概述了爱德华曲线方程和有限域K上点运算，在参数d不是k平方的情况下，是完备的，即没有异常点以及相同点操作也是一致的（对比之前的椭圆曲线点加法规则（有无穷远点，相同点操作异与不同点），这样的性质可以增强对侧信道攻击（side channel attack）的抵御能力，同时点乘的效率也更高！
写在前面
上一节说了sm2公钥恢复过程，重在原理，具体代码有待测试优化！
本文开始要讲椭圆曲线中的另外一类：爱德华曲线。 这种曲线的规则跟之前所说的均有所不同。secp256k1,sm2，secp256r1 都属于Weierstrass曲线系列。 接下来的几篇思路为：爱德华曲线 --> 扭曲爱德华曲线 --> ed25519签名 目标是在区块链应用中已经采用的ed25519签名，但是由于采用的是新曲线，所以很有必要讲讲背景知识，下面开启新一段旅程！
爱德华曲线
爱德华曲线（Edwards curves）是另一类椭圆曲线族。 是美国数学家Harold Edwards 在2007研究提出的。曲线方程：
$x^2+y^2=1+dx^2y^2$
或者
$x^2+y^2=c^2(1+dx^2y^2)$
定义在有限域K上,满足c, d ∈ K 且 cd(1 − $c^4$·d) ≠ 0.
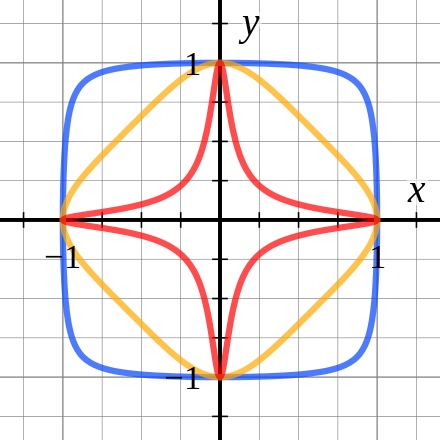
下图是一条实数域上的爱德华曲线： $x^2+y^2=1-d\cdot x^2\cdot y^2$
红色线参数 d = 300, 黄色线参数d = $\sqrt{8}$，蓝色线参数 d = −0.9
曲线点运算
像Weierstrass曲线上的点群一样，爱德华曲线上的点也构成一个交换群，点与点可以相加，标量相乘。
爱德华曲线点相加公式如下：
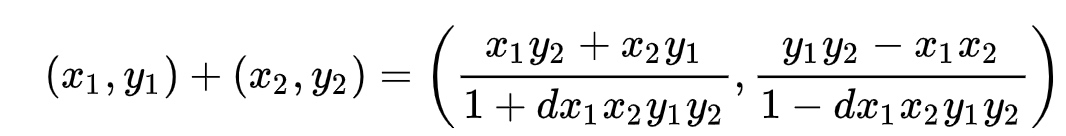
点$(x_1,y_1)$的逆是$(-x_1,y_1)$，群“零元”表示为(0, 1)，由于坐标不全是0，“零元”称呼字面表达不确切，所有又称为“中性点”。性质就是零元性质，群中元素P + (0,1) = P, P + (-P) = (0,1)
根据以上加法规则，可以看出(0, −1) 阶为2, 点(±1,0) 阶是4. 爱德华曲线的特殊之处在于总有一个点阶为4.
举例说明
令d = 2, 方程为：$x^2+y^2=1+2x^2y^2$
任取一点P = (1,0)，易见P在曲线上，计算P + （0，1）= $(x_3,y_3)$根据上述加法规则：
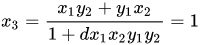
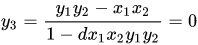
即P + （0，1）= $(x_3,y_3)$= （1，0）= P 同时检验了中性点（0，1）的性质！其他点可自行选取尝试计算。
特殊地，如果两个点相同，则公式变为:
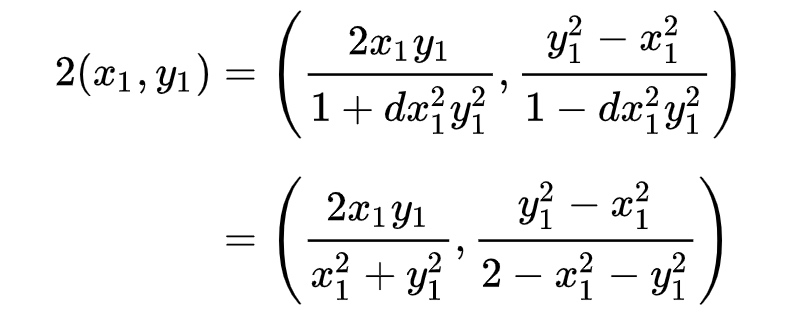
小结
本文简要概述了爱德华曲线方程和有限域K上点运算，在参数d不是k平方的情况下，是完备的，即没有异常点以及相同点操作也是一致的（对比之前的椭圆曲线点加法规则（有无穷远点，相同点操作异与不同点），这样的性质可以增强对侧信道攻击（side channel attack）的抵御能力，同时点乘的效率也更高！
好了，下一篇继续说爱德华曲线的更多内容！
欢迎关注公众号：blocksight
