区块链中的数学 - 多项式承诺
- blocksight
- 发布于 2021-02-22 17:35
- 阅读 10721
目前为止的方案中, 承诺方造假的问题依然存在,仔细研究会发现问题关键在于承诺方P知道计算的输入变量r,z, 这样就有机会构造出新的多项式在r,z处取特定的值。如果P不知道r,z,就不能这样作弊了。于是Kate承诺选择在密文空间中进行计算。
写在前面
上一篇介绍了Pedersen 密钥分享, 本文继续讲密码学承诺中重要的成员--多项式承诺诺!
多项式承诺诺在零知识证明中应用比较广泛,且有多种形式。本文介绍Kate版本的多项式承诺。
何为多项式
多项式
首先我们需要知道什么是多项式?这个比较简单,以单变量多项式为例说明:
$f(x)=a_0 + a_1x + ... + a_nx^n ={a_0,a_1,...,a_n}$
以上是系数表示形式,系数序列确定多项式也就确定了。 还有一种表示方法是使用n+1点值对表示n次多项式。
$f(x)={(x_0,y_0),(x_1,y_1), ... ,(x_n,y_n)}$
同样,这种方法也能唯一确定多项式。
两种表示方法,各有其应用场景,比如系数表示法在计算多项式相加的场合效率高,而点值表示法则应用在多项式相乘计算场合。
由于两种表示法本质是同一个东西,所以二者可以相互转化,其中FFT就是实现系数表达到点值表示的转换方法,而IFFT正好相反。关于FFT和IFFT深入解读超出本文范围,可自行查阅。
多项式承诺
多项式承诺有多种方式,比如最直接的就是把多项式系数承诺出去,这样多项式在承诺后就不能再改变了。 这种方式在系数较少即多项式度数较低时适用。
当系数比较多(比如超过10万)承诺结果就会比较大,增加存储与传输的代价。 能不能用点值方式做承诺呢?最好适用一个点的值,因为点值用的多了同样也会有上述问题。
一个原始的点值承诺方法浮出水面:
点值承诺
- 承诺生成(Commit)阶段: 承诺方选择一个暂不公开的多项式,在某一点r处,计算出对应的承诺c并公开。c = f(r), 将(r,c)公开给验证方
- 承诺披露(Reveal)阶段: 承诺方公布多项式,验证方根据多项式计算r处值c' = f(r),比较c'= c,一致则表示验证成功,否则失败。
这种原始承诺方式有问题吗?仔细想想容易发现有以下问题: 在r处取值为c的多项式存在多个,比如f(r) = c,g(r) = c ,那么承诺方就可以在承诺时候使用多项式f(x),而在打开验证阶段使用g(x)也能通过验证,这样就达不到承诺的目的了。
这种把多项式和盘托出的打开方式成为全部打开,还有一种部分打开的方式:
- 承诺生成(Commit)阶段: 承诺方选择一个暂不公开的多项式,在某一点r处,计算出对应的承诺c并公开。c = f(r), 将(r,c)公开给验证方
- 挑战(challenge)与证明生成: 验证方V随机选择一个数z,发给承诺方P, P计算在z处值s = f(z),同时计算出t(x) = f(x)-s / (x-z),计算t(x)在z处的值w = t(z)(w也称为见证witness) 返回给验证方V(s,w)
- 验证阶段: 验证方验证:s = f(z) --> f(z) - s = 0 --> 方程f(x)-s = 0 有根x=z, 即存在t(x) 使得f(x) - s = t(x)(x - z), 这个方程是恒等式,所以任意点都成立。 在r处自然也是成立的,所以可以检验f(r) - s = t(r)(r - z) = c - s = w(r - z ) 通过则验证成功,否则失败。
流程图如下:
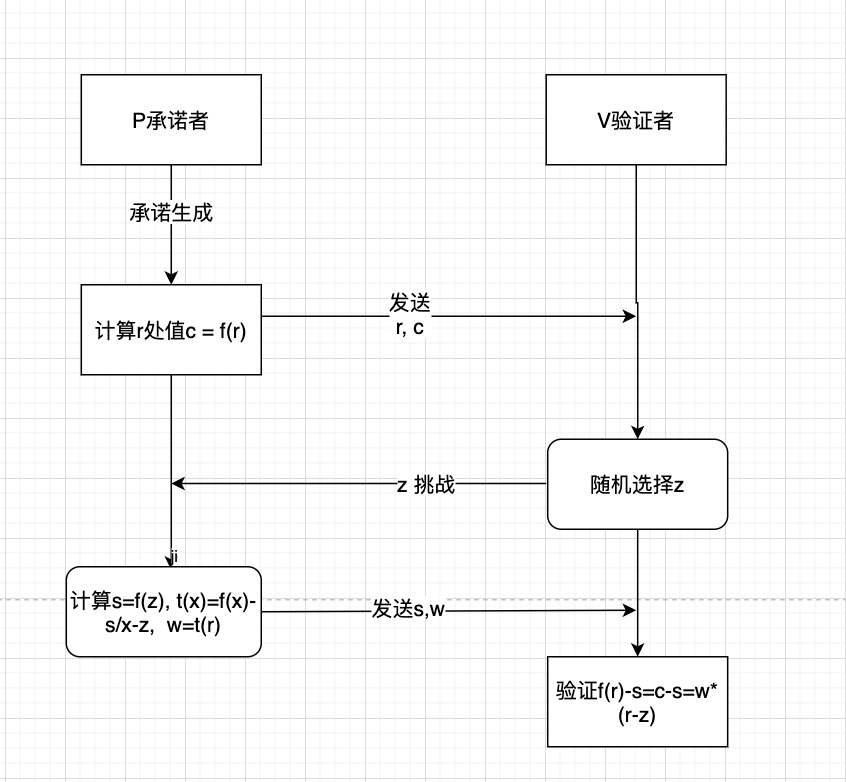
这种方法采用部分打开方式验证,使得多项式增加了隐私性,自始至终没有完全暴露最初的多项式。现在已经比较接近Kate承诺的方案了!
小结
目前为止的方案中, 承诺方造假的问题依然存在,仔细研究会发现问题关键在于承诺方P知道计算的输入变量r,z, 这样就有机会构造出新的多项式在r,z处取特定的值。如果P不知道r,z,就不能这样作弊了。于是Kate承诺选择在密文空间中进行计算。
好了,下一篇继续Kate承诺的余下部分!
原文链接:https://mp.weixin.qq.com/s/P3UUaZzN8Egt0pZhKiXYZg 欢迎关注公众号:blocksight
相关阅读
区块链中的数学 - Pedersen密钥共享 Pedersen 密钥分享
区块链中的数学 - Pedersen承诺 密码学承诺--Pedersen承诺
区块链中的数学 - 哈希承诺 密码学承诺--hash承诺
区块链中的数学 - 不经意传输 不经意传输协议
区块链中的数学- BLS 基石(双线性函数)和配对 双线性映射(配对)
区块链中的数学 - BLS门限签名 BLS m of n门限签名
区块链中的数学 - BLS密钥聚合 BLS密钥聚合
区块链中的数学 - BLS数字签名 BLS签名及验证
区块链中的数学 - 参与者 < 门限值t的密钥更新Amir Herzberg方案 Amir Herzberg改进方案
区块链中的数学 - Feldman的可验证的密钥分享 Feldman可验证密钥分享方案
区块链中的数学 - Ed25519签名 Ed25519签名
区块链中的数学-ElGamal算法 ElGamal算法签名及验证&实例演练
Schorr签名与椭圆曲线 Schorr签名与椭圆曲线
区块链中的数学-Uniwap自动化做市商核心算法解析 Uniwap核心算法解析(中)
- Uniswap v3 数学洞察系列翻译 —— 第六部分 共 6 部分 3836 浏览
- Uniswap v3 数学洞察系列翻译 —— 第五部分 共 6 部分 3944 浏览
- Uniswap v3 数学洞察系列翻译 —— 第四部分 共 6 部分 4383 浏览
- Uniswap v3 数学洞察系列翻译 —— 第三部分 共 6 部分 5239 浏览
- Uniswap v3 数学洞察系列翻译 —— 第二部分 共 6 部分 3345 浏览
- Uniswap v3 数学洞察系列翻译 —— 第一部分 共 6 部分 3925 浏览
- stark数学基础和翻译名词 3250 浏览
- 区块链中的数学--PLookup 7281 浏览
- 区块链中的数学 -- MultiSet check& Schwartz–Zippel lemma 6785 浏览
- 区块链中的数学 - 环签名(ring signature) 16084 浏览
- 区块链中的数学 -盲签名(Blind Signature) 13870 浏览
- 区块链中的数学 - sigma协议OR Proof&签名 7798 浏览

