区块链中的数学-爱德华曲线运算的几何意义
- blocksight
- 更新于 2020-10-24 23:16
- 阅读 8663
本文介绍了爱德华曲线运算的几何意义，引入了扭曲爱德华曲线。
写在前面
上一节说了爱德华曲线基本方程和点运算规则，由于Edwards curve是新的曲线，本文继续说下更多内容
点运算几何表述
前面我们说了Weierstrass曲线上两点相加的几何意义，是通过两点连接一条直线，与曲线相交第三个点关于x轴的对称点就是所求的和。 爱德华曲线也可以结合几何表示。
令$x^2+y^2 = 1 $表示单位圆，$P_1(x_1,y_1),P_2(x_2,y_2)$ , 是圆上两个点，见下图：
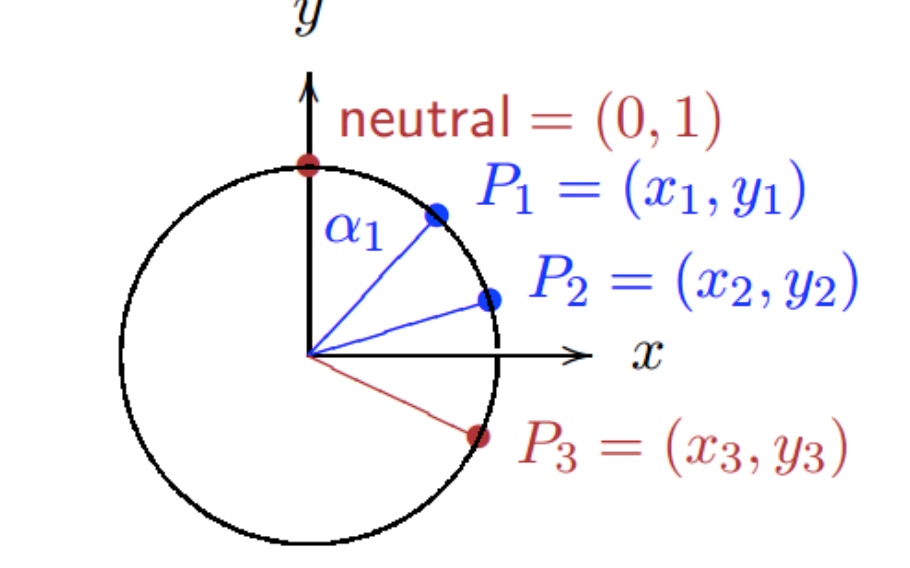
$(x_1,y_1)=(sin(\alpha_1),cos(\alpha_1)),(x_2,y_2)=(sin(\alpha_2),cos(\alpha_2))$, = (sin(α), cos(α)), 两点相加等于弧度相加后的坐标： $x3 =sin(\alpha_1+\alpha_2)=sin(\alpha_1)cos(\alpha_2)+cos(\alpha_1)sin(\alpha_2)=x_1y_2+y_1x_2$
$y3 =cos(\alpha_1+\alpha_2)=cos(\alpha_1)cos(\alpha_2)+sin(\alpha_1)sin(\alpha_2)=y_1y_2-x_1x_2$
现在单位元曲线换成爱德华曲线： $x^2+y^2 = 1+x^2y^2$(d = 1)
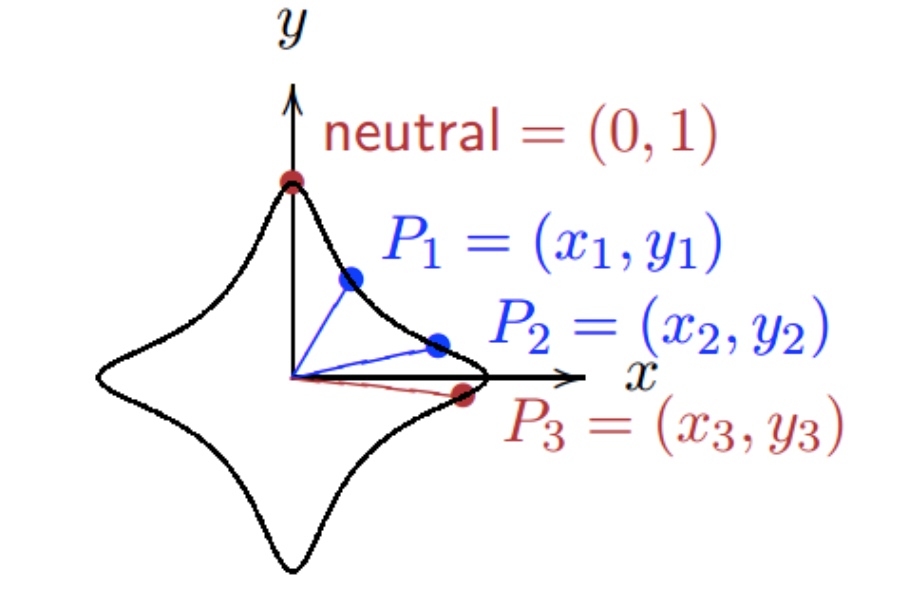
$x_3=\frac{x_1y_2+x_2y_1}{1+x_1x_2y_1y_2}$
$y_3=\frac{y_1y_2-x_1x_2}{1-x_1x_2y_1y_2}$
扭曲爱德华曲线
爱德华曲线稍加变化得到扭曲的爱德华曲线（Twisted Edwards curves），方程：
$ax^2+y^2=1+dx^2y^2$
满足a, d ≠ 0 且 a ≠ d.
下图是在实数域上方程$10x^2+y^2=1+6x^2y^2$ 的曲线
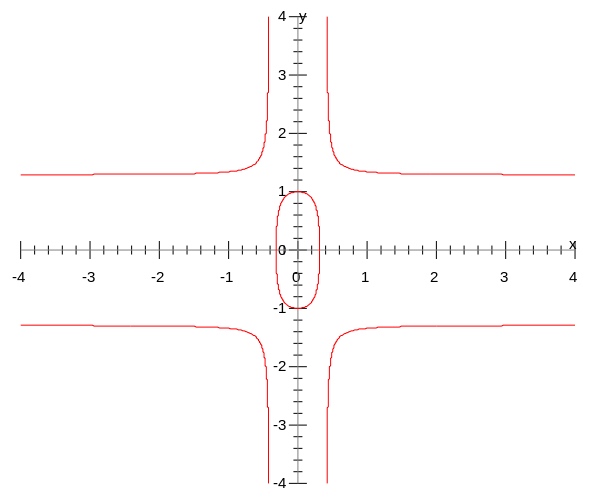
扭曲爱德华曲线方程多了一个系数a, 相对应的点加法运算有细微变化：
$x_3=\frac{x_1y_2+x_2y_1}{1+dx_1x_2y_1y_2}$
$y_3=\frac{y_1y_2-ax_1x_2}{1-dx_1x_2y_1y_2}$
x坐标计算不变，y坐标添加了a系数因子。
如果两个相同点相加公式变为：
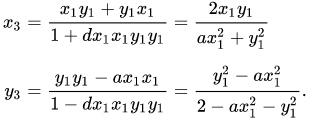
有了扭曲爱德华曲线，正常的爱德华曲线可以看成扭曲爱德华曲线的特例（a = 1 的情况下），即每一条爱德华曲线都是扭曲爱德华曲线。
为什么要有扭曲的爱德华曲线呢？ 大体两个方面：
-
范围：爱德华曲线在有限域上阶为4限制了曲线的数量，使用扭曲方式进行扩展，所有蒙哥马利曲线(Montgomery Curve)都可以有理映射成扭曲爱德华曲线.
-
性能：更大范围曲线使用快速的加法公式，一些爱德华曲线可以通过扭曲来加速运算
以上优点都可以例证推理说明，涉及到知识点很多，感兴趣的可以自己查阅文后参考资料。
小结
本文介绍了爱德华曲线运算的几何意义，引入了扭曲爱德华曲线。我们只说了平面坐标系下的运算，还有射影坐标系的运算规则和含义以及各种运算的定量分析，论证爱德华曲线运算的快速，这些内容可参考： https://christianepeters.files.wordpress.com/2012/10/20080620-rennes.pdf
https://hal.archives-ouvertes.fr/hal-01942759/document
https://en.wikipedia.org/wiki/Edwards_curve
同时，本文中提到了蒙哥马利曲线，也是椭圆曲线的一种形式，所以我们说椭圆曲线的内容虽然讲了很多，但远未结束，不过我们聚焦区块链中使用相关的，从应用角度，简单学习原理也可以，不必深究！
好了，下一篇继续介绍蒙哥马利曲线和Curve25519！
欢迎关注公众号：blocksight
