区块链中的数学 - 不经意传输

blocksight
更新于 2021-01-16 22:43
阅读 9146

不经意传输（Oblivious transfer）或者译为茫然传输是密码学中的一类协议，缩写为OT，实现了发送方将潜在的许多信息中的一个传递给接收方，但对接收方所接收信息保持未知状态。

## 写在前面

上一篇讲述了[双线性映射（配对）](https://learnblockchain.cn/article/1963)的性质，关于其如何在椭圆曲线群上加以实现，以后有机会在详述。
从本文开始，我们要进入零知识证明的范畴，零知识证明是密码学重要分支，尤其区块链快速发展的这几年，零知识证明技术在隐私，layer2扩容等方面发挥着关键的作用。

但是零知识证明涉及到众多的密码学，数学相关知识，包括公钥密码体制，椭圆曲线，不经意传输，同态加密，密码学承若，电路，甚至安全多方计算等。

前面的章节对应公钥密码体制，椭圆曲线进行了说明，总体上循序渐进。现在是不错的时候继续深入了。
还是那句话千里之行，一步都不能少，捷径走多了，一定会在某个地方摔跟头！

所以如果你现在看到这篇文章，想继续学习了解的话， 建议把之前文章大致看下。

本文将介绍零知识证明技术众多的基础知识之一  ---- 不经意传输

## 不经意传输

不经意传输的最早是由Michael O.Rabin在1981年提出的。这个版本的不经意传输发送方会有 1/2 的概率将消息发送给接收方，而发送方不知道接收方是否接收到该消息。到1985年，较为实用的二选一方案被Shimon Even,Oded Goldreich等人提出。
这个版本的不经意传输模型中，A每次发两条信息$(m_1,m_2)$给B，B提供一个输入，并根据输入获得输出信息，在协议结束后，B得到了自己想要的那条信息（或者），而A并不知道B最终得到的是哪条。B除了得到的那条信息，对其他信息也一无所知。

下面我们以基于RSA加密算法来描述这种不经意传输方案。

## 1 out 2方案

假设A有两个消息,B实现茫然选择其一。

流程图：

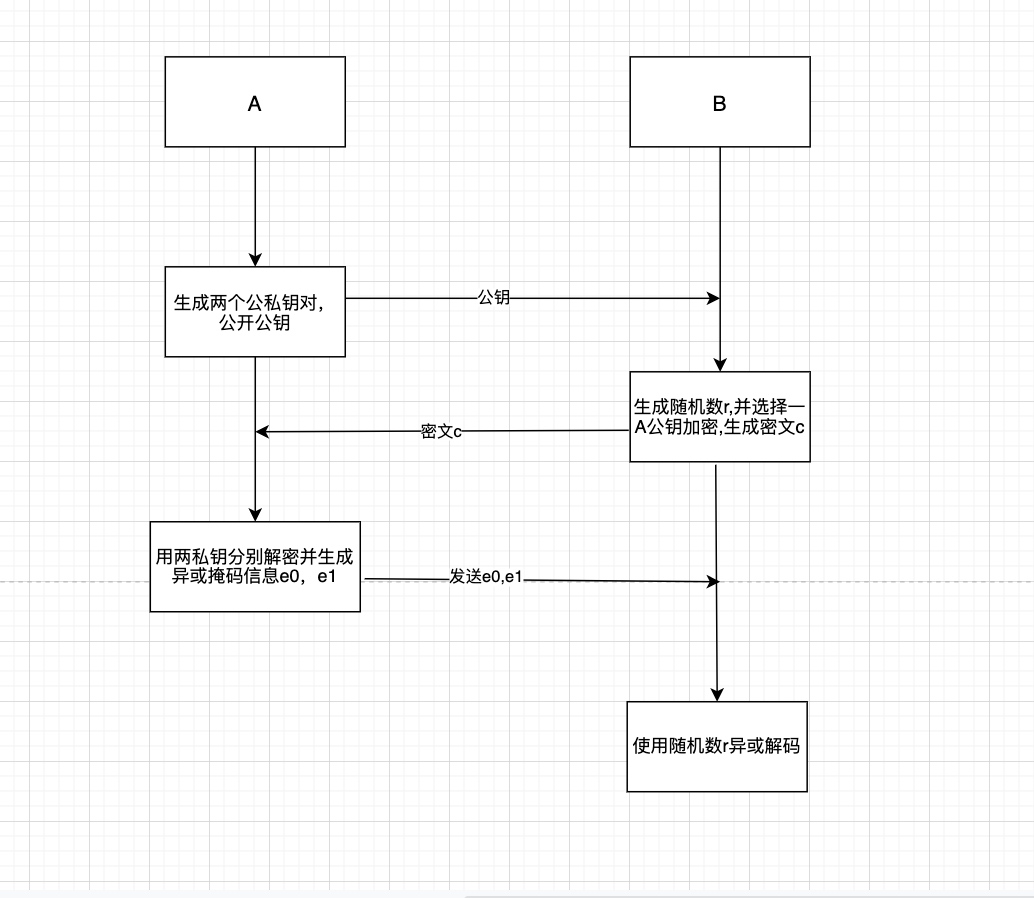
![](https://img.learnblockchain.cn/2021/01/18/16109348617152.jpg)

流程介绍：

1. 发送者A生成两对rsa公私钥（）（,，公开两个公钥、。
2. B生成随机数r，并用两个公钥之一加密随机数.
   例如如果想要得到消息$m_0$就用$pk_0$加密随机数，如果想要得到$m_1$就用$pk_1$加密随机数，c = Encrypt(r),并将密文c发送给A。
3. A用自己的两个私钥分别解密收到随机数密文，得到两个解密结果:
   $k_0=Decrypt(c,x_0)$
   $k_1=Decrypt(c,x_1)$
   并将两个结果分别与两条信息进行异或，生成掩码消息
   $e_0=k_0 \bigoplus m_0$
   $e_1=k_1 \bigoplus m_1$
   并将两个结果$e_0，e_1$发给B。
4. B用之前生成的随机数r与收到的$e_0，e_1$分别做异或操作，得到的两个结果中只有一条为真实数据，另外一条为随机数。
   $m'_0=e_0 \bigoplus r$
   $m'_1=e_1 \bigoplus r$
   B在步骤2中，如果使用$pk_0$加密，得到$m'_0=m_0$的反之是$m_1$

该协议的安全性在于步骤3中，A无法知晓B的随机r, 从而对b的最终选择也就无从知晓。

同理，1 out n多选一不经意传输也可基于类似原理实现，只需要将2换成n秘钥。

## 小结

不经意传输的原理还是简单明了的，其具体实现也可以结合其他加密算法。

好了，下一节继续讲paillier加密及其同态运算！

欢迎关注公众号：blocksight

### 相关阅读：

[区块链中的数学- BLS 基石（双线性函数）和配对](https://learnblockchain.cn/article/1963)    双线性映射（配对）

[区块链中的数学 - BLS门限签名](https://learnblockchain.cn/article/1962)    BLS m of n门限签名

[区块链中的数学 - BLS密钥聚合](https://learnblockchain.cn/article/1912)    BLS密钥聚合

[区块链中的数学 - BLS数字签名](https://learnblockchain.cn/article/1905)  BLS签名及验证

[区块链中的数学 - 参与者 < 门限值t的密钥更新Amir Herzberg方案](https://learnblockchain.cn/article/1843)   Amir Herzberg改进方案

[区块链中的数学 - Feldman的可验证的密钥分享](https://learnblockchain.cn/article/1789)   Feldman可验证密钥分享方案

[区块链中的数学 - Ed25519签名](https://learnblockchain.cn/article/1663)   Ed25519签名

[区块链中的数学-ElGamal算法](https://learnblockchain.cn/article/1557)  ElGamal算法签名及验证&实例演练

[区块链中的数学-VRF基于ECC公钥体制的证明验证过程](https://learnblockchain.cn/article/1582)   基于椭圆曲线的VRF证明验证过程

[Schorr签名与椭圆曲线](https://learnblockchain.cn/article/2450)   Schorr签名与椭圆曲线

[区块链中的数学-Uniwap自动化做市商核心算法解析](https://learnblockchain.cn/article/1494) Uniwap核心算法解析（中）

写在前面

上一篇讲述了双线性映射（配对）的性质，关于其如何在椭圆曲线群上加以实现，以后有机会在详述。从本文开始，我们要进入零知识证明的范畴，零知识证明是密码学重要分支，尤其区块链快速发展的这几年，零知识证明技术在隐私，layer2扩容等方面发挥着关键的作用。

前面的章节对应公钥密码体制，椭圆曲线进行了说明，总体上循序渐进。现在是不错的时候继续深入了。还是那句话千里之行，一步都不能少，捷径走多了，一定会在某个地方摔跟头！

所以如果你现在看到这篇文章，想继续学习了解的话，建议把之前文章大致看下。

本文将介绍零知识证明技术众多的基础知识之一 ---- 不经意传输

不经意传输

不经意传输的最早是由Michael O.Rabin在1981年提出的。这个版本的不经意传输发送方会有 1/2 的概率将消息发送给接收方，而发送方不知道接收方是否接收到该消息。到1985年，较为实用的二选一方案被Shimon Even,Oded Goldreich等人提出。这个版本的不经意传输模型中，A每次发两条信息$(m_1,m_2)$给B，B提供一个输入，并根据输入获得输出信息，在协议结束后，B得到了自己想要的那条信息（或者），而A并不知道B最终得到的是哪条。B除了得到的那条信息，对其他信息也一无所知。