Tornado Cash 的工作原理（开发者逐行解析）

Tornado Cash 介绍

Tornado cash 是一个加密货币智能合约混合器，使用户能够将加密货币存入一个地址并从另一个钱包中取出，而不在这两个地址之间创建可追踪的链接。

Tornado cash 可能是最具代表性的零知识智能合约应用程序，因此我们将以足够低的水平解释它的工作原理，以便程序员可以重现该应用程序。

假设读者知道 Merkle 树如何工作，并且对反转 cryptographic hash 是不可行的。读者还应当被假定至少具有 Solidity 的中级水平（因为我们将会阅读源代码片段）。

Tornado Cash 是一个相对先进的智能合约，因此如果你仍然对该语言不熟悉，请先查看我们的 Solidity 教程。

Tornado Cash 的快速警告

法律问题

Tornado Cash 目前受到美国政府的制裁，进行互动可能会“玷污”你的钱包，并导致以后与中心化交易所交互时标记来自该钱包的交易。

2024 更新：截至 2024 年 11 月 28 日，制裁已由美国上诉法院解除。

Tornado Cash 黑客事件

5 月 27 日， Tornado Cash 治理智能合约（不是我们在这里回顾的智能合约）被黑客攻击，攻击者通过通过了一个恶意提案，从而获得了治理的绝大多数 ERC20 投票代币 ERC20 投票代币用于治理。此后，他们已 收回控制权，留下一小部分给自己。

零知识如何运行（对于厌恶数学的程序员）

你可以在不知道零知识证明算法的情况下理解 Tornado Cash 如何工作，但你必须知道零知识证明的工作原理。与它们的名字和许多流行示例相反，零知识证明证明的是计算的有效性，而不是某个事实的知识。它们并不进行计算。它们取一个商定的计算、一个证明该计算已执行的证明和该计算的结果，然后确定证明者是否真的进行了计算并得出了输出。零知识部分来自于一种可选特性，即计算证明可以以一种不提供输入信息的方式表示。

例如，你可以展示你知道一个数的质因数，而不透露它们，使用 RSA 算法。RSA并不声称“我知道两个秘密数字”；相反，它证明你将两个隐藏的数字相乘并生成了公钥。RSA 加密实际上只是零知识证明的一个特例。在 RSA 中，你证明你知道两个相乘以生成你公钥的秘密素数。在零知识中，你将这种“神秘乘法”推广到任意的算术和布尔运算。一旦我们有了对基本运算的零知识操作，我们可以构建关于更奇特的事物的零知识证明，比如证明我们知道哈希函数的原像、Merkle 根，甚至一个完全功能的虚拟机。

另一个要点：零知识证明验证并不进行计算，它只验证某人是否进行了计算并提交了声称的输出。

还有一个有用的推论：要生成一个计算的零知识证明但不验证，你必须实际进行计算。

这有什么道理？你怎么能证明你知道哈希的原像，而不实际对原像进行哈希呢？因此，证明者确实进行计算并创建一些称为证明的辅助数据，以确认他们确实正确地进行了计算。

当你验证 RSA 签名时，你没有将他人的私钥因素相乘来生成他们的公钥，这对目的来说是徒劳的。你只需验证签名和消息是否匹配，使用一个单独的算法。因此，一个计算由以下内容组成：

verifier_algorithm(proof, computation, public_output) == true

在 RSA 的上下文中，你可以认为公钥是计算的结果，而签名和消息是零知识证明。

计算和输出都是公开的。我们同意我们在使用某个哈希函数并得到了某个输出。证明“隐藏”了使用的输入，仅证明哈希函数已执行并生成了输出。

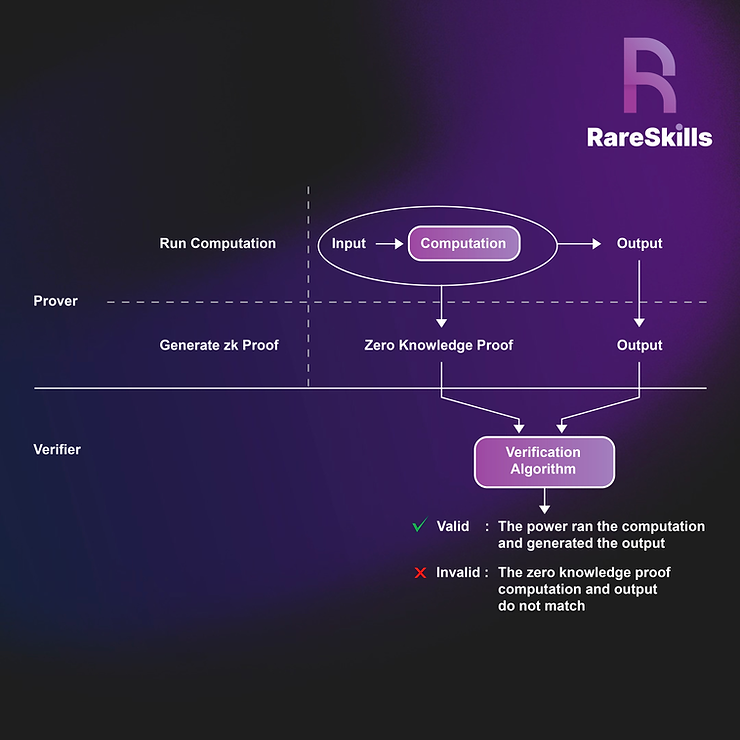
仅凭证明，验证者无法计算 public_output。验证步骤并不进行计算，它仅验证基于证明的声称计算产生的公共输出。

我们在本文中不会教授零知识算法，但只要你能接受我们可以证明计算发生而不自己进行计算，那我们就好继续进行。

匿名加密货币转账如何工作：混合

从根本上讲，Tornado Cash 的匿名化策略是混合，这类似于其他匿名加密货币如 Monero。多个用户将他们的加密货币提交到一个地址，将他们的存款“混合”在一起。然后他们以一种方式提取这些存款，以确保存款者和撤回者无法相互关联。

想象一下 100 个人将一美元纸币投入一个堆中。然后 100 个不同的人在一天后出现，各自提取一美元。在这个方案中，我们并不知道最初的存款者试图将钱发送给谁。

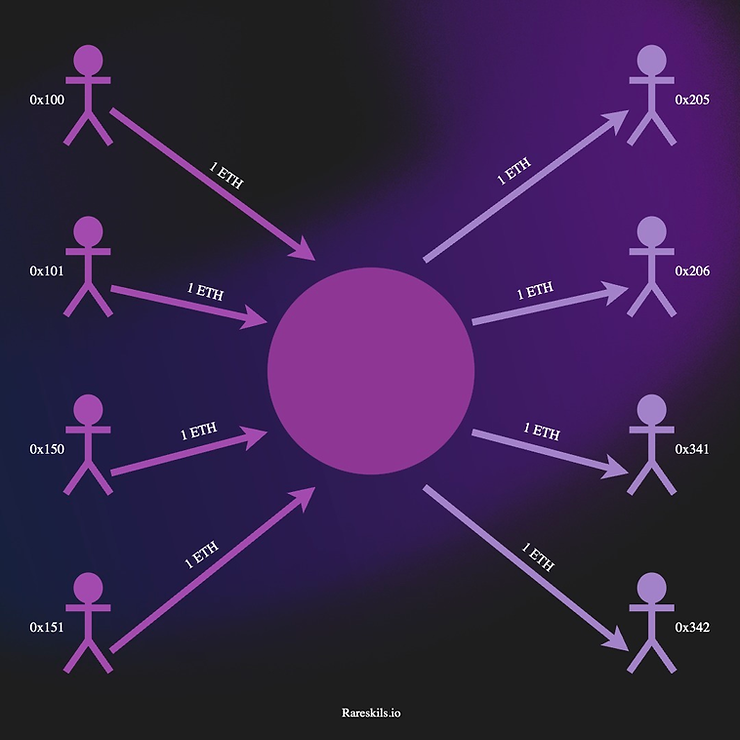
显然，存在一个问题：如果任何人都可以从这堆现金中提取现金，那么它将很快被盗。但如果我们试图留下有关谁被允许撤回的某些元数据，那么这将透露出存款者试图将钱发送给谁。

混合永远无法完全私密

当你将以太坊发送到 Tornado Cash 时，这是完全公开的。当你从 Tornado Cash 提取时，这也完全是公开的。公开的是什么，两者之间的地址无法关联（假设有足够多的其他存款者和撤回者）。

人们能知道的关于一个地址的事情是“这个地址是从 Tornado Cash 获得以太的”或“这个地址向 Tornado Cash 存入了资金”。当一个地址从 Tornado Cash 中撤回时，人们无法确定加密货币是来自哪个存款者。

没有零知识的 Tornado Cash：大量逻辑 OR 的哈希原像证明

让我们尝试在不担心隐私的情况下解决这个问题。

存款者创建两个秘密数字，将它们连接在一起，并在存入以太时将在链上放置其哈希（稍后我们将讨论为什么我们生成两个秘密数字而不是一个）。当几个人存款时，在智能合约中存在几个公共哈希，我们不知道原像是什么。

撤回者出现，撤回者揭示了其中一个哈希的原像（这两个秘密数字）并提取他们的存款。

这显然失败，因为它显示存款者与撤回者之间进行了链下秘密数字的通讯。

然而，如果撤回者可以证明他们知道 一个哈希 的原像，而不揭示 哪个哈希是 和 不揭示该哈希的原像，那么我们就有了一个功能完整的加密货币混合器！

最天真的解决方案是创建一次循环计算，在循环中遍历所有哈希：

zkproof_preimage_is_valid(proof, hash_{1}) OR 
zkproof_preimage_is_valid(proof, hash_{2}) OR
zkproof_preimage_is_valid(proof, hash_{3}) OR
...
zkproof_preimage_is_valid(proof, hash_{n-1}) OR
zkproof_preimage_is_valid(proof, hash_{n}) 

记住，验证者实际上并没有进行上述计算，因此我们不知道哪个哈希是有效的。验证者（Tornado Cash）只是验证证明者进行了上述计算，并且返回了真值。返回真实的方法无关紧要，只有这样返回的才有意义；它只能在证明者知道某个原像的情况下返回真实。

在这里要重要的是：所有存款哈希都是公开的。当用户存款时，他们提交两个秘密数字的哈希，该哈希是公开的。我们试图掩盖的是撤回者知道哪个哈希的原像。

但这是一个很大的计算。包含大量存款的大循环是非常昂贵的。[1]

我们需要一个数据结构能够紧凑地存储大量哈希，幸运的是我们有：Merkle 树。

使用 Merkle 树存储大量哈希

与其在所有哈希中循环遍历，我们可以说“我知道一个哈希的原像”并且“该哈希在 Merkle 树中”。这达成了与指向一个很长的哈希数组并说“我知道其中一个哈希的原像”相同的目的，只是更加高效。

Merkle 证明在树的大小上是对数级的，因此比我们之前的庞大循环多了些额外的工作。

当加密货币被存入时，用户生成两个秘密数字，连接它们，哈希它们，并将该哈希放入 Merkle 树中。

在撤回时，撤回者提供一个叶子哈希的原像，然后通过 Merkle 证明证明该叶子哈希存在于树中。

这当然将存款者与撤回者关联在一起，但如果我们在零知识的方式中同时进行 Merkle 证明和叶子原像验证，那么链接就破裂了！

零知识证明让我们证明我们针对公众 Merkle 根生成了有效的 Merkle 证明以及叶子的原像，而不需要展示我们如何进行该计算。

仅提供一个零知识证明证明拥有 Merkle 证明和生成根是不够安全的，撤回者还必须证明他们知道叶子的原像。

Merkle 树的叶子都是公开的。每当有人存款时，他们都会提供一个存储在公共中的哈希。由于 Merkle 树是完全公共的，任何人都可以计算任何叶子的 Merkle 证明。

因此，证明一个叶子在树中并不足以防止通过证明伪造带来的盗窃。

撤回者还必须隐私地证明有关该叶子的原像，而不揭示该叶子。请记住，叶子本身是两个数字的哈希。

你可以看到 存款函数 中的 _commitment 参数是公开的。_commitment 变量是添加到树的叶子，它是两个秘密数字的哈希，而存款者并不公开。

/**
  @dev 将资金存入该合约。调用者必须发送（对于 ETH）或批准（对于 ERC20）等于或 `denomination` 的值。
  @param _commitment 注释承诺，即 PedersenHash(nullifier + secret)
**/
function deposit(bytes32 _commitment) external payable nonReentrant {
    require(!commitments[_commitment], "该承诺已被提交");

    uint32 insertedIndex = _insert(_commitment);
    commitments[_commitment] = true;
    _processDeposit();

    emit Deposit(_commitment, insertedIndex, block.timestamp);
}

实际上，撤回的证明包括证明以下计算已执行：

processMerkleProof(merkleProof, hash(concat(secret1, secret2))) == root

这里 processMerkleProof 将 Merkle 证明和叶子作为参数，而 hash(concat(secret1, secret2)) 产生的则是叶子。

在 Tornado Cash 的上下文中，验证者是 Tornado Cash 智能合约，它将向提供有效证明的人转移资金。

证明者是撤回者，他们可以证明他们进行哈希计算以产生其中一个叶子。一般而言，唯一可以撤回的人是存款者，因为他们将是唯一能证明他们知道哈希原像的参与者。当然，这个用户必须使用一个不同且完全不相关的地址进行撤回！

撤回者实际上执行上述计算（Merkle 证明和叶子哈希生成），生成 zk-proof 以证明他们正确地进行了操作，然后将此证明提供给智能合约。

merkleProof 和 {secret1, secret2} 在证明中是隐藏的，但凭借计算证明，验证者可以验证撤回者实际上运行了该计算以正确生成叶子和 Merkle 根。

所以让我们总结一下：

• 存款者：
  • 生成两个秘密数字并从它们的连接中创建承诺哈希
  • 提交一个承诺哈希
  • 向 Tornado Cash 转移加密货币
• Tornado Cash：
  • 在存款阶段：
    • 将承诺哈希添加到 Merkle 树中
• 撤回者：
  • 为 Merkle 根生成有效的 Merkle 证明
  • 从两个秘密数字生成承诺哈希
  • 生成上述计算的 zk-proof
  • 向 Tornado Cash 提交证明
• Tornado Cash
  • 在撤回阶段：
    • 验证证明是否与 Merkle 根匹配
    • 将加密货币转移到撤回者

防止多次撤回

上述方案存在一个问题：什么阻止我们进行多次撤回？显然，我们需要“移除” Merkle 树中的叶子，以便记录已撤回的存款，但这将揭示哪个存款是我们的！

Tornado cash 通过不从 Merkle 树中移除叶子来处理此问题。一旦叶子添加到 Merkle 树中，它将永远留在那里。

为了防止多次撤回，智能合约使用一种称为“nullifier 方案”的机制，这在零知识应用和协议中非常常见。

Nullifier 方案

在零知识中，nullifier 方案类似于一种独特的 nonce，提供了一层匿名性。

很明显，为什么叶子由两个秘密数字构成，而不是一个。

输入存款哈希的两位数字是 nullifier 和一个秘密，叶子的哈希是 concat(nullifier, secret) 的哈希，顺序是这样的。

在撤回过程中，用户必须提交 nullifier 的哈希，也就是 nullifierHash，并证明他们连接了 nullifier 和 secret，并对其进行了哈希以生成其中一个叶子。智能合约可以使用零知识算法验证发送者真的知道 nullifier 哈希的原像。

nullifier 哈希被添加到一个映射中，以确保它不会被重用。

这就是我们需要两个秘密数字的原因。如果我们揭示了这两个数字，那么我们就会知道撤回者所针对的哪个叶子！通过仅揭示一个组成数字，无法确定其关联的叶子。

记住，零知识证明验证无法给出私密输入的 nullifier，仅能验证计算、输出和证明是否一致。这就是用户必须提交公共 nullifierHash 和证明，他们从隐藏的 nullifier 中计算出的原因。

你可以在 Tornado Cash 的 withdraw 函数 中看到这个逻辑。

让我们总结一下。用户必须证明：

• 他们知道叶子的原像
• nullifier 未被之前使用过（这只是一个简单的 solidity 映射，而不是一个 zk 验证步骤）
• 他们可以生成 nullifier 哈希和 nullifier 的原像

以下是可能的结果：

• 用户提供错误的 nullifier：检查 nullifier 和 nullifier 原像的 zk 证明将不通过
• 用户提供错误的 secret：叶子原像的 zk 证明将不通过
• 用户提供错误的 nullifier 哈希（以绕过第 86 行的检查）：nullifier 和 nullifier 原像的 zk 证明将不通过

增量 Merkle 树是一个省 gas 的 Merkle 树

你可能注意到，在上述解释中，我们快得过于简单了。如何在链上更新 Merkle 树而不耗尽 gas？存款量很可能是很多，计算整个过程的成本是难以承受的。

增量 Merkle 树通过一些巧妙的优化来解决这些限制。但在探讨优化之前，我们需要理解限制。

增量 Merkle 树是一棵固定深度的 Merkle 树，每个叶子开始时都是零值，通过逐一替换从左到右的零叶来添加非零值。

下面的动画演示了一棵深度为 3 的增量 Merkle 树，最多可以容纳 8 个叶子。遵循我们对 Tornado Cash 的域术语，我们称这些为“承诺”，标记变量 Ci。

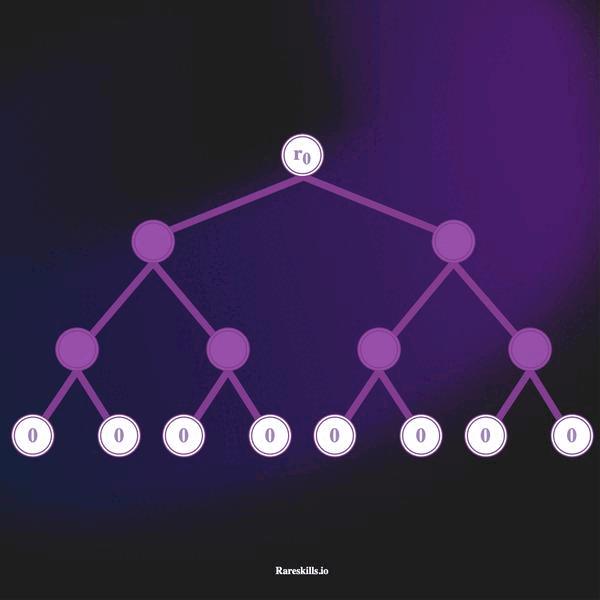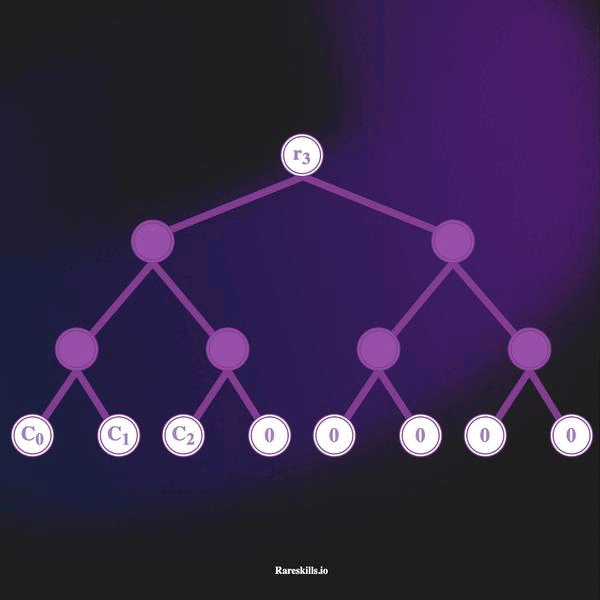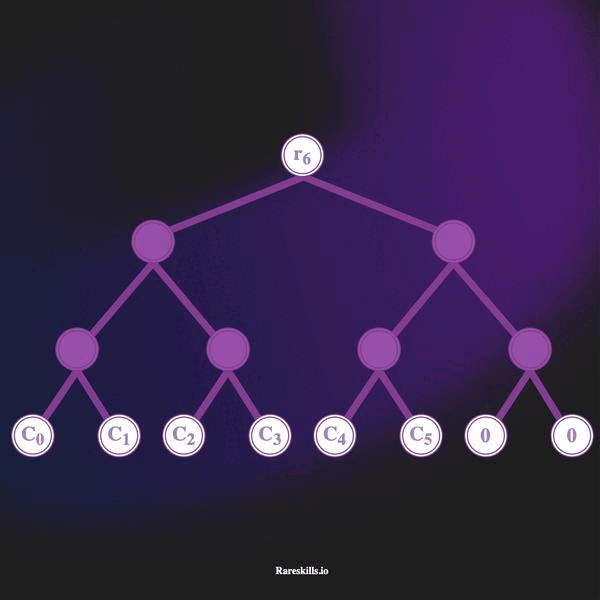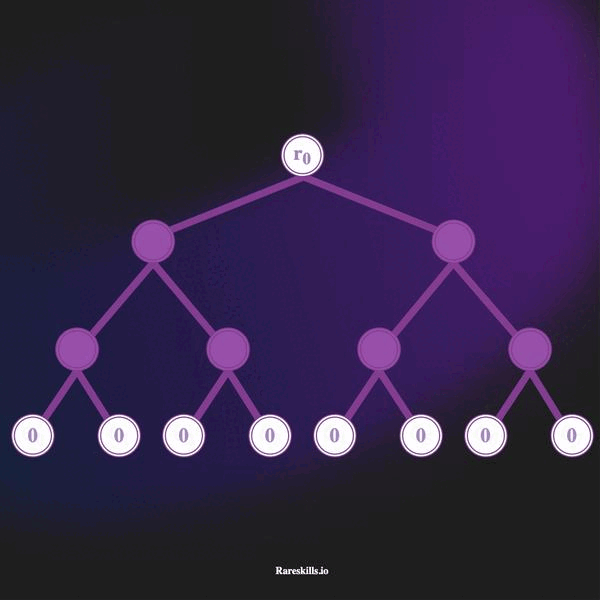
以下是增量 Merkle 树的一些重要特性：

• Merkle 树的深度固定为 32。这意味着它无法处理超过 2^32 - 1 的存款。（这是 Tornado Cash 所选的一个任意深度，但需要保持恒定）。
• Merkle 树开始时是一棵所有叶子均为 hash(bytes32(0)) 的树。
• 随着存款的进行，最左侧未使用的叶子将被承诺哈希覆盖。存款以“从左到右”的方式添加到叶子中。
• 一旦存款被添加到 Merkle 树中，则无法移除。
• 每进行一次新存款便会存储一个新的根。Tornado Cash 将其称为“带历史的 Merkle 树”。因此，Tornado Cash 存储的是一系列 Merkle 根，而不是单一的根。显然，Merkle 根在成员添加时会发生变化。

现在我们面临一个问题：在链上构建一棵有 2^32 - 1 叶子的 Merkle 树将耗尽 gas。仅仅计算第一个层面就需要超过 400 万次迭代，这显然是行不通的。

但增量 Merkle 树的限制使得有两个关键不变量使智能合约能够进行大规模的计算捷径：当前节点右侧的所有内容都是预测高度的 Merkle 子树，其中所有根都是零，而且当前节点左侧的所有内容可以被缓存而不是重新计算。

巧妙的捷径 1：所有新成员右侧的子树均包含所有零叶子的 Merkle 子树

所有零叶子的 Merkle 子树具有可预测的根，可以预先计算。

由于所有叶子都以零开头，我们输入到构建 Merkle 树中的大量工作将包括计算所有叶子为零的 Merkle 树。

请查看下面的图像，并注意当所有叶子为零时，计算量重复多少：

大多数叶子对将会是 bytes32(0) 和 bytes32(0) 的连接。然后该哈希将与来自姐妹子树的相同哈希连接，依此类推。

Tornado Cash 预计算了一棵深度为零的树（仅是一个 `bytes32(0) 叶子的哈希）、包含两叶零的子树根，包含四叶零的子树根，包含八叶零的子树根等。

这意味着我们可以预先计算一棵具有高度为零、子树叶子全为零的 Merkle 树的 Merkle 根，最高高度为 31（记住，Merkle 树的高度是固定的）。

对于所有可能高度的 Merkle 子树，其中的叶子全是零，Tornado Cash 将会预先计算。以下是 Tornado Cash 的带历史的 Merkle 树 中的预先计算列表：

  /// @dev 提供了一个 MiMC MerkleTree 的零（空）元素。最多 32 层
  function zeros(uint256 i) public pure returns (bytes32) {
    if (i == 0) return bytes32(0x2fe54c60d3acabf3343a35b6eba15db4821b340f76e741e2249685ed4899af6c);
    else if (i == 1) return bytes32(0x256a6135777eee2fd26f54b8b7037a25439d5235caee224154186d2b8a52e31d);
    else if (i == 2) return bytes32(0x1151949895e82ab19924de92c40a3d6f7bcb60d92b00504b8199613683f0c200);
    else if (i == 3) return bytes32(0x20121ee811489ff8d61f09fb89e313f14959a0f28bb428a20dba6b0b068b3bdb);
    else if (i == 4) return bytes32(0x0a89ca6ffa14cc462cfedb842c30ed221a50a3d6bf022a6a57dc82ab24c157c9);
    else if (i == 5) return bytes32(0x24ca05c2b5cd42e890d6be94c68d0689f4f21c9cec9c0f13fe41d566dfb54959);
    else if (i == 6) return bytes32(0x1ccb97c932565a92c60156bdba2d08f3bf1377464e025cee765679e604a7315c);
    else if (i == 7) return bytes32(0x19156fbd7d1a8bf5cba8909367de1b624534ebab4f0f79e003bccdd1b182bdb4);
    else if (i == 8) return bytes32(0x261af8c1f0912e465744641409f622d466c3920ac6e5ff37e36604cb11dfff80);
    else if (i == 9) return bytes32(0x0058459724ff6ca5a1652fcbc3e82b93895cf08e975b19beab3f54c217d1c007);
    else if (i == 10) return bytes32(0x1f04ef20dee48d39984d8eabe768a70eafa6310ad20849d4573c3c40c2ad1e30);
    else if (i == 11) return bytes32(0x1bea3dec5dab51567ce7e200a30f7ba6d4276aeaa53e2686f962a46c66d511e5);
    else if (i == 12) return bytes32(0x0ee0f941e2da4b9e31c3ca97a40d8fa9ce68d97c084177071b3cb46cd3372f0f);
    else if (i == 13) return bytes32(0x1ca9503e8935884501bbaf20be14eb4c46b89772c97b96e3b2ebf3a36a948bbd);
    else if (i == 14) return bytes32(0x133a80e30697cd55d8f7d4b0965b7be24057ba5dc3da898ee2187232446cb108);
    else if (i == 15) return bytes32(0x13e6d8fc88839ed76e182c2a779af5b2c0da9dd18c90427a644f7e148a6253b6);
    else if (i == 16) return bytes32(0x1eb16b057a477f4bc8f572ea6bee39561098f78f15bfb3699dcbb7bd8db61854);
    else if (i == 17) return bytes32(0x0da2cb16a1ceaabf1c16b838f7a9e3f2a3a3088d9e0a6debaa748114620696ea);
    else if (i == 18) return bytes32(0x24a3b3d822420b14b5d8cb6c28a574f01e98ea9e940551d2ebd75cee12649f9d);
    else if (i == 19) return bytes32(0x198622acbd783d1b0d9064105b1fc8e4d8889de95c4c519b3f635809fe6afc05);
    else if (i == 20) return bytes32(0x29d7ed391256ccc3ea596c86e933b89ff339d25ea8ddced975ae2fe30b5296d4);
    else if (i == 21) return bytes32(0x19be59f2f0413ce78c0c3703a3a5451b1d7f39629fa33abd11548a76065b2967);
    else if (i == 22) return bytes32(0x1ff3f61797e538b70e619310d33f2a063e7eb59104e112e95738da1254dc3453);
    else if (i == 23) return bytes32(0x10c16ae9959cf8358980d9dd9616e48228737310a10e2b6b731c1a548f036c48);
    else if (i == 24) return bytes32(0x0ba433a63174a90ac20992e75e3095496812b652685b5e1a2eae0b1bf4e8fcd1);
    else if (i == 25) return bytes32(0x019ddb9df2bc98d987d0dfeca9d2b643deafab8f7036562e627c3667266a044c);
    else if (i == 26) return bytes32(0x2d3c88b23175c5a5565db928414c66d1912b11acf974b2e644caaac04739ce99);
    else if (i == 27) return bytes32(0x2eab55f6ae4e66e32c5189eed5c470840863445760f5ed7e7b69b2a62600f354);
    else if (i == 28) return bytes32(0x002df37a2642621802383cf952bf4dd1f32e05433beeb1fd41031fb7eace979d);
    else if (i == 29) return bytes32(0x104aeb41435db66c3e62feccc1d6f5d98d0a0ed75d1374db457cf462e3a1f427);
    else if (i == 30) return bytes32(0x1f3c6fd858e9a7d4b0d1f38e256a09d81d5a5e3c963987e2d4b814cfab7c6ebb);
    else if (i == 31) return bytes32(0x2c7a07d20dff79d01fecedc1134284a8d08436606c93693b67e333f671bf69cc);
    else revert("索引超出范围");
}

在计算 Merkle 根时，我们总是知道我们处于“z 级”，可以简单地获取全部叶子为零的预计算 Merkle 子树根。

关于“零根”的技术性细节

Tornado Cash 实际上并不使用 hash(bytes32(0)) 作为空值，而是使用 hash("tornado")。这并不影响算法，因为它只是一个常量。然而，使用零值的概念来讨论增量 Merkle 树会更有意义。

巧妙的捷径 2：所有新成员左侧的子树由其根可以缓存而不是重新计算

考虑我们添加第二个存款的情况。我们已经计算了第一个存款的哈希。那个哈希会被缓存到一个 Tornado Cash 称作 filledSubtrees 的映射中。filledSubtree 仅仅是 Merkle 树中所有叶子均为非零值的子树。我们将在下面的动画中称之为 fs：

重点是，只要你需要左侧的中间哈希，它已经为你计算完成。

这个精彩的特点是由于不允许更改或移除叶子的限制。有了填充承诺的子树，它再也不需要重新计算。

现在让我们进行概括。我们不要把左侧节点看作“首个存款”，而是把它自身看作一棵子树的根。

在最极端的情况下，考虑我们在最后一个叶子进行存款。在我们左侧会是以第二个最后一个叶子（第 0 深度），在那边左侧会是深度为 1 的子树（带 4 个叶子），在那边左侧会是深度为 2 的子树（带 8 个叶子），等等。在最极端的情况下，最多不会多于 32 颗这样的树。

组合捷径

我呢们左侧的所有节点是填充子树（即使只是一个叶子），而我们右侧的所有节点总是零叶或包含所有零叶子的子树。由于左侧根已被缓存，并且右侧根由深度 n 的所有零子树预计算，因此我们可以高效地在任何级别上计算任何中间哈希连接，并在链上生成一个深度为 32 的 Merkle 树，仅通过 32 次迭代。 这虽然不便宜，但也是可行的。与 400 万次计算相比，确实好得多！

向左散列或向右散列？

但随着我们“走向根”，我们如何知道必须以何种顺序连接子树的哈希？

例如，我们假设取用一个新的承诺哈希并将其增加为叶子。在上方节点中，我们是否应该将其连接为 new_commitment | other_value 还是 other_value | new_commitment？

这里有个小窍门：每个偶数索引节点都是左子节点，而每个奇数索引节点都是右子节点。这对叶子节点以及树的每一层都是正确的。下面的图是可以观察到这一模式的。

让我们直观地理解这个模式。如果正在插入的是第 0 个叶子，我们在达到根的时候只会向右散列。0 ÷ 2 将保持为 0，而 0 是偶数。为了根据之上的定义，偶数总会散列到右边。

再考虑极端情况，当插入的为最后一个叶子的时候，必须始终往左散列到根。在这一过程中每个节点都是奇数。这种模式适用于所有中间节点；从叶子节点的索引开始，不断除以二，在我们上升树的过程中会告诉我们是否处于左子节点或右子节点。以下动画说明了当我们在奇数节点时往左散列，在偶数节点时往右散列：

因此，在任意层次上，我们都知道我们哈希的相关关系。

因此，我们需要以下两个信息：

• 正在插入的节点索引
• 当前索引是偶数还是奇数

以下是 Tornado Cash 源代码的屏幕截图使用这些信息。这个循环在层次中一次遍历以根据刚添加的新叶子重新生成 Merkle 根。

总结一下，更新链上的 Merkle 根时，我们：

• 在新索引处添加一个叶子，将当前索引设置为 currentIndex
• 向上移动一个层次，将 currentIndex 设置为 currentIndex 除以 两。然后，
  • 如果 currentIndex 是奇数则用 filledSubtree 向左散列
  • 如果 currentIndex 是偶数则用 precomputed 的零树向右散列。

能够将这样一个非平凡算法压缩成一个小的 Solidity 表达式真是太酷了。

Tornado Cash 存储最后 30 个根，因为随着每次存款，根会不断变化

每当插入一项时，Merkle 根肯定会改变。如果撤回者为最新的根创建 Merkle 证明（记住，叶子都是公开的），但先发送来的存款交易又改变了根，则 Merkle 证明将不再有效。zk 验证者算法确保 Merkle 证明的有效证明与当前根一致，因此如果根改变，证明将无法通过。

为了给撤回者一些时间提取他们的交易，他们可以参考最多 30 个根。

这个变量 roots 是一个 uint256 到 bytes32 的映射。当 Merkle 证明达到根时（循环完成后），它会存储在 roots 中。currentRootIndex 限制在最大值（30）的情况下逐步增加，达到最大值后则会覆盖根的索引零。因此，它表现得像一个固定大小的队列。以下是 Tornado Cash 的 Merkle 树代码中 _insert 函数的片段。在重新计算根后，以以上描述的方式将其存储。

增量 Merkle 树的存储变量

以下是增量 Merkle 树的历史能够正常工作的存储变量。

mapping(uint256 => bytes32) public filledSubtrees;
mapping(uint256 => bytes32) public roots;
uint32 public constant ROOT_HISTORY_SIZE = 30;
uint32 public currentRootIndex = 0;
uint32 public nextIndex = 0;

• filledSubtrees 是我们已经计算的子树（即所有叶子均为非零值）
• roots 是最近的 30 个根
• currentRootIndex 从 0 到 29 的数字，以索引至 roots
• nextIndex 是用户调用存款时将要填充的当前叶子。用户在调用 deposit 进行 Tornado Cash 交易时，会调用 _insert() 来更新 Merkle 树，然后调用 _processDeposit()。

function deposit(bytes32 _commitment) external payable nonReentrant {
    require(!commitments[_commitment], "该承诺已经提交");

    uint32 insertedIndex = _insert(_commitment);
    commitments[_commitment] = true;
    _processDeposit();

    emit Deposit(_commitment, insertedIndex, block.timestamp);
}

_processDeposit() 仅确保金额是准确的（仅能存入 0.1、1 或 10 以太币，具体取决于你与之交互的 Tornado Cash 实例）。以下是这一非常简单操作的代码。

function _processDeposit() internal override {
    require(msg.value == denomination, "请和交易一起发送 `mixDenomination` ETH");
}

超级优化的 MiMC 哈希

要在链上计算 Merkle 根，必须使用哈希算法（显然），但 Tornado Cash 并没有使用传统的 keccak256；而是使用 MiMC。

为什么会这样有点超出范围，但原因在于某些哈希在零知识证明生成方面的计算成本比其他哈希更低。MiMC 的设计就是为了“对 zk 友好”，而 keccak256 则不是。“对 zk 友好”意味着该算法自然映射到零知识证明算法表示计算的方式。

但这造成了一个有趣的悖论，因为新节点添加时必须在链上计算 MiMC 来重新计算根，而以太坊没有预编译的 zk 友好的哈希合约。（也许你可以为此撰写一个 EIP？）

因此，Tornado Cash 团队在原始字节码中自行编写了 MiMC Hasher。如果你查看 Tornado Cash 在 Etherscan 的合约验证，你会看到一个警告：

Etherscan 无法验证原始字节码与 Solidity 的关系，因为 MiMC 哈希并未用 Solidity 编写。

Tornado Cash 团队将 MiMC Hasher 部署为一个单独的 智能合约。要使用 MiMC 哈希，Merkle 树代码会对该合约进行跨合约调用。如下面代码所示，这些是 静态调用，因为接口将其定义为纯，因而 Etherscan 显示它没有交易历史。

interface IHasher {
    function MiMCSponge(uint256 in_xL, uint256 in_xR) external pure returns (uint256 xL, uint256 xR);
}

我们根据上文引用的 Tornado Cash 代码知道这是“接口”。 (github 链接)。

在 circom 库的 github 问题 中，你可以看到有关为什么该代码没有 Solidity 版本的理由，即使有汇编块：直接操控栈是不可能的。

（附言：非常低级的密码算法是 Huff 语言一个很好的用例，你可以通过我们的 Huff 语言难题 来学习它）。

将自己的哈希函数作为原始字节码部署

circomlib js 存储库包含用于创建原始字节码哈希的 JavaScript 工具。以下是生成 MiMC 和 Poseidon Hash 的代码。

从 Tornado Cash 提现

首先，用户必须使用 updateTree 脚本 在本地重构 Merkle 树。该脚本将下载所有相关的 solidity 事件 并重构 Merkle 树。然后，用户将生成 Merkle 证明和叶子承诺预影像的零知识证明。如前所述，Tornado Cash 存储最近的 30 个 Merkle 根，所以用户应该有充足的时间提交他们的证明。如果用户生成证明并等待太久，他们将必须重新生成证明。

Tornado Cash 合约会检查

1. 提交的 nullifierHash 之前未被使用
2. 根是在根历史（最近的 30 个根）中
3. 零知识证明是否有效：a. 隐藏哈希预影像是否生成了叶子 b. 用户实际上知道 nullifierHash 预影像 c. 用户创建了一个 Merkle 证明，该证明使用了生成提案根的那棵叶子。 d. 提议的根是最后 30 个根之一（这在 Solidity 代码中公开进行了检查）

以下是以上步骤的可视化：

了解了这一点后，下面是 Tornado Cash 提现函数的代码，应当自解释。

function withdraw(bytes calldata _proof,
    bytes32 _root,
    bytes32 _nullifierHash,
    address payable _recipient,
    address payable _relayer,
    uint256 _fee,
    uint256 _refund
  ) external payable nonReentrant {
    require(_fee <= denomination, "费用超过转账金额");
    require(!nullifierHashes[_nullifierHash], "该凭证已经被使用");
    require(isKnownRoot(_root), "无法找到你的 merkle 根"); // 确保使用最近的根
    require(
      verifier.verifyProof(
        _proof,
        [uint256(_root), uint256(_nullifierHash), uint256(_recipient), uint256(_relayer), _fee, _refund]
      ),
      "无效的提取证明"
    );

    nullifierHashes[_nullifierHash] = true;
    _processWithdraw(_recipient, _relayer, _fee, _refund);
    emit Withdrawal(_recipient, _nullifierHash, _relayer, _fee);
  }

上述的 _relayer、_fee 和 _refund 与支付给可选交易中继者的费用有关，我们将很快解释。

函数 isKnownRoot(root) 验证提议的根是最后 30 个根之一

这是一个简单的 do-while 循环，从当前索引（最后一个活动叶子）向后循环，以查看提交给提现函数的根是否在根历史中。（github 链接）

由于回溯仅为 30，因此我们不必担心不受限制的循环耗费过多气体。

/**
@dev 判断根是否存在于根历史中
*/function isKnownRoot(bytes32 _root) public view returns (bool) {
    if (_root == 0) {
      return false;
    }
    uint32 _currentRootIndex = currentRootIndex;
    uint32 i = _currentRootIndex;
    do {
      if (_root == roots[i]) {
        return true;
      }
      if (i == 0) {
        i = ROOT_HISTORY_SIZE; // 30
      }
      i--;
    } while (i != _currentRootIndex);
    return false;
}

Circom 代码用于定义零知识证明计算

本节描述用于生成验证 ZK 证明的电路的 circom 代码。如果你对 Circom 不熟悉并想学习，请查看我们的 零知识难题 在 Circom 中。

然而，我们仍将尝试从高层次解释 Circom 代码。

Circom 并未在区块链上执行，它被转译成可怕的 Solidity 代码，你可以在 Tornado Cash 的 Verifier.sol 中看到。它看起来如此吓人是因为它实际上是在执行 zk-proof 验证的数学运算。幸运的是，Circom 要易读得多。

在这里我们有三个组件：HashLeftRight 组合哈希，DualMux（它只是 MerkleTreeChecker 的一个工具）和 MerkleTreeChecker。MerkleTreeChecker 接受 leaf、root 和 proof。proof 有两个部分：pathElements（姐妹子树的 Merkle 根）和 pathIndices（指示电路知道在该级别上连接哈希的顺序）。

最后一行，root === hashers[levels - 1].hash 是最终确定根以匹配 leaf 和 proof 的地方。

请记住，nullifierHash 是 nullifier 的哈希，而 commitment 是 nullifier 和 secret 的哈希。此计算的 Circom 表述如下。尽管可能难以阅读，但应清楚输入是 nullifier 和 secret，输出是 commitment 和 nullifierHash。

现在我们可以进入零知识算法的核心

一个私有信号意味着它是“隐藏在证明中”的，使用了早先的命名法。

在上面的代码中，代码验证了 nullifier 哈希计算是否有效。然后承诺预影像和 Merkle 证明被提供给之前的 MerkleTree 验证器。

如果一切正常，verifier 将返回 true，表示证明有效，匿名地址可以提现。

防止提现中的前运行攻击

安全研究人员可能注意到 Solidity 代码没有防御前运行攻击。当有人向内存池提交有效的零知识证明时，是什么防止有人复制该证明并将提现地址替换为他们自己的？

这是我们为了简单起见忽略的东西，但 Withdraw.circom 文件包括虚拟信号，平方接收者（以及中继者所需的其他参数）。这意味着 zk-proof 必须还要证明提取者平方了接收者的地址并得到了其地址的平方（请记住，地址只是 20 字节的数字）。计算地址的平方并计算 nullifier 和 secret 的哈希是一个计算，因此获取这些部分的任何错误都会使整个证明无效。

什么是中继者和费用？

中继者是一个链外机器人，代表其他用户支付Gas费以换取某种形式的付款。Tornado Cash 的提取者通常希望使用全新的地址以增强隐私，但全新的地址没有任何Gas支付提现。

为了解决这个问题，提取者可以请求中继者执行交易，以换取收到一部分 Tornado Cash 提现。

中继者的提现地址也必须使用上述描述的前运行保护，这可以在上面的代码截图中看到。

deposit() 和 withdrawal() 的总结

当调用 deposit 时：

• 用户提交 hash(concat(nullifier, secret))，以及他们正在存入的加密货币。
• Tornado Cash 验证存入的金额符合其接受的面值。
• Tornado Cash 将承诺添加到下一个叶子。叶子不会被删除。

当调用 withdraw 时：

• 用户基于 Tornado Cash 发出的事件重构 Merkle 树
• 用户必须提供 nullifier 的哈希（公开）、他们正在验证的 Merkle 根以及集中证明他们知道 nullifier、 secret 和 Merkle 证明的 zk 证明
• Tornado Cash 验证 nullifier 之前未被使用
• Tornado Cash 验证提议的根是最后 30 个根之一
• Tornado Cash 验证零知识证明

没有什么能阻止用户提交一个无意义的叶子而没有已知的预印象。在这种情况下，提交的加密货币将永远滞留在合同中。

智能合约架构的快速概览

以下是构成 Tornado Cash 的智能合约

Tornado.sol 是一个抽象合约，实际上由 ERC20Tornado.sol 或 ETHTornado.sol 实现，具体取决于部署是否旨在混合 ERC20 或特定面值的 ETH。不同的 ETH 面值和 ERC20 代币各有自己的 Tornado Cash 实例。

MerkleTreeWithHistory.sol 包含我们之前详细讨论的 _insert() 和 isKnownRoot() 功能。

Verifier.sol 是 Circom 电路的 Solidity 转译输出。

cTornado.sol 是用于治理的 ERC20 代币，不是核心协议的一部分。

Tornado Cash 改善Gas效率的地方

总体来看，Tornado Cash 的架构非常优秀，但仍有一些 Gas优化 的机会。

• Tornado Cash 对预计算的全零叶子的 Merkle 子树进行线性查找，但这可以通过硬编码二分搜索以更少的操作完成。
• Tornado Cash 经常使用 uint32 作为堆栈变量；uint256 将是更好的选择，以避免 EVM 进行隐式转换。
• Tornado Cash 有一些不必要修改为 public 的常量。公共常量除非智能合约要读取它们，否则没有必要，并且会增加智能合约的大小。
• 前缀操作符 (++i) 比后缀操作符 (i++) 更省气，并且 Tornado Cash 可以在不影响逻辑的情况下更改此操作。
• nullifierHashes 是一个公共映射，但它也经过一个公共查看函数 isSpent() 封装。这是冗余的。

结论

就这样；我们已经调查了 Tornado Cash 的 整个 代码库，并对每个变量和函数的作用有了很好的理解。Tornado Cash 在相对较小的代码库中嵌入了令人印象深刻的复杂性。我们在这里探讨了几个重要的技术，包括：

• 使用零知识证明来证明对哈希预印象的知识而不泄露预印象
• 如何在链上使用增量 Merkle 树
• 如何使用从原始字节码编码的自定义哈希函数
• 如何运作拉引器方案
• 如何匿名提取
• 如何防止零知识证明 dapps 被前运行攻击

RareSkills

这些材料是我们 零知识课程 的一部分。有关一般智能合约开发，请查看我们的 Solidity Bootcamp 以获取专业的 Solidity 开发者。我们提供最严格、最新的智能合约训练项目。

澄清说明

[1] 任何熟悉 ZK 电路的人都知道我们不能创建任意长度的 for 循环。电路必须在创建时适应非常大的数组。然而，仍然可以准确地说，“循环”遍历这么多哈希是计算上昂贵的，因为这相当于创建一个令人无法忍受的大电路。

最初发布于 2023 年 6 月 27 日

• 原文链接： rareskills.io/post/how-d...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～