对数大小的承诺证明

在前面的章节中，我们展示了将向量 $\mathbf{a}$ 和 $\mathbf{G}$ 的元素总和相乘可以计算外积项的总和，即 $\sum \mathbf{a}\otimes\mathbf{G}=\sum\mathbf{a}\sum\mathbf{G}$。我们还展示了外积在其主对角线上“包含”了内积。

要“提取”内积 $\langle\mathbf{a},\mathbf{G}\rangle$，必须从外积中减去所有不是内积部分的项，即下面的紫色阴影区域：

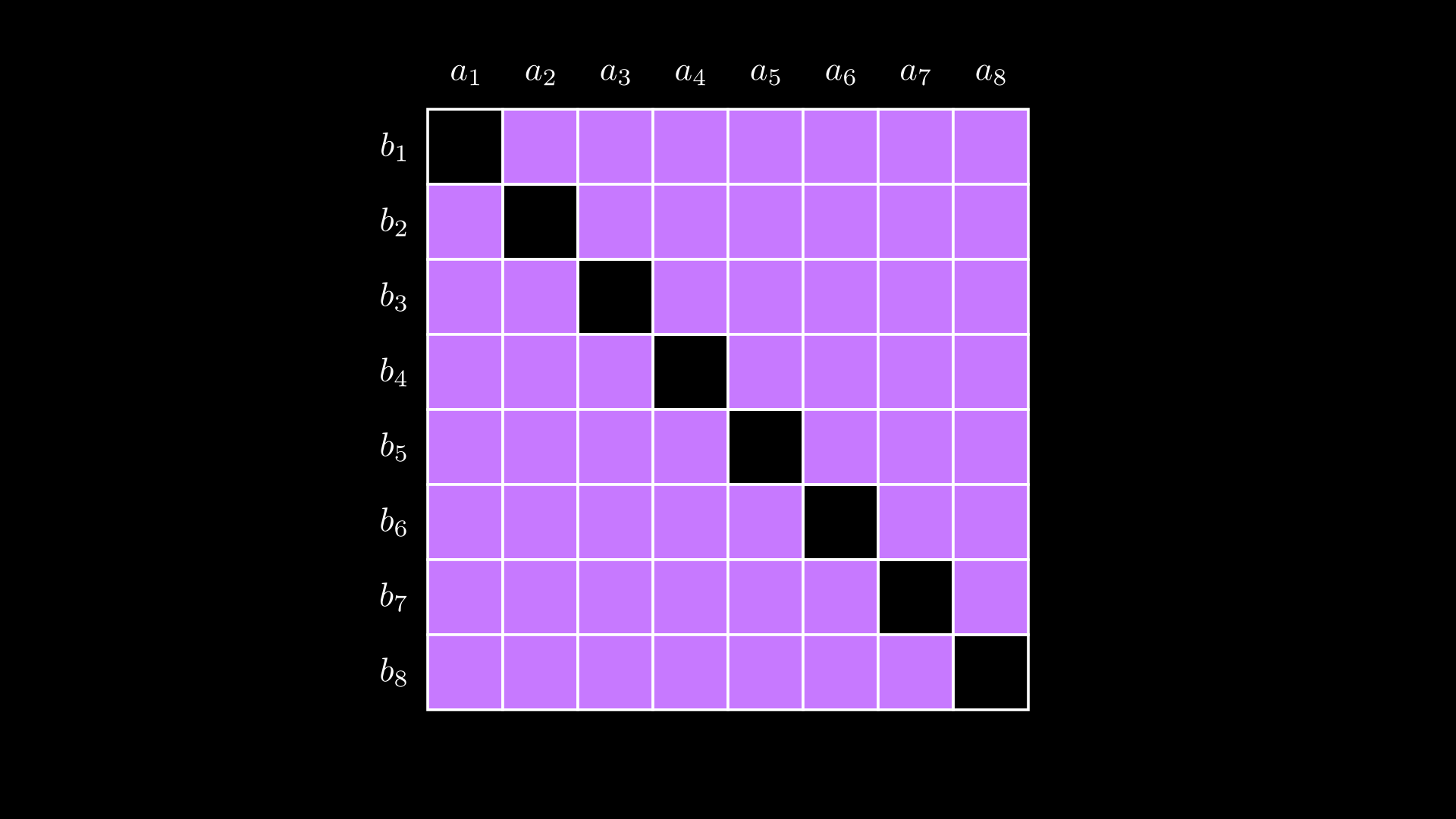
有 $\mathcal{O}(n^2)$ 这样的项，因此直接执行这一操作效率不高。

然而，观察到我们可以以下面动画所示的方式“填充外积”：

https://img.learnblockchain.cn/2025/02/27/MatrixFoldingAnimation.mp4

在上面的动画中，当证明者发送非对角线项后，证明者将 $\mathbf{G}$ 和 $\mathbf{a}$ 同时折叠，使得它们的长度减少一半。

最后，当我们对 $\mathbf{a}$ 和 $\mathbf{G}$ 折叠 $\log n$ 次后，向量的大小为 1。 当 $n=1$ 时，外积等于内积，我们只需透露这两个向量，它们将是常数大小。

回顾 — 这与前一章算法的关系

之前，我们展示了如何证明我们知道承诺 $P$ 的开口，同时只发送 $n/2$ 个元素而不是 $n$。作为回顾：

证明者将向量 $\mathbf{a}$ 承诺给 $P$，即 $P = \langle\mathbf{a},\mathbf{G}\rangle$。然后，证明者发送非对角线项 $L=a_1G_2 + a_3G4 + \dots a{n-1}G_n$ 和 $R = a_2G_1 + a_4G_3 + \dots anG{n-1}$。验证者回应 $u$，证明者将向量 $\mathbf{a}$ 根据 $u$ 折叠为 $\mathbf{a}’=\mathsf{fold}(\mathbf{a},u)=[a_1u+a_2u^{-1}, a_3u+a4u^{-1}, \dots, a{n-1}u+a_nu^{-1}]$ 并将 $\mathbf{a}’$ 发送给验证者。由于 $\mathbf{a}’$ 的长度为 $n/2$，我们将传输的数据大小减少了一半。

验证者然后检查 $\langle\mathsf{fold}(\mathbf{G},u^{-1}),\mathbf{a}’\rangle\stackrel{?}=Lu^2+P+Ru^{-2}$

该算法的最初目的是通过展示我们知道内积 $P$ 的和以及非对角线项 $L$ 和 $R$ 的和等于 $\mathbf{a}$ 和 $\mathbf{G}$ 的成对分区外产品的元素之和来证明我们知道对 $P$ 的承诺。

如果我们递归地应用这个算法，我们得到了本章开始时描述的 $\log n$ 算法。

然而，我们也可以将该过程解释为我们证明我们知道承诺 $P’$ 的开口，其中 $P’=(Lu^2+P+Ru^{-2})$，关于基向量 $\mathsf{fold}(\mathbf{G},u^{-1})$ 的长度为 $n’=n/2$。我们可以幼稚地通过发送 $\mathbf{a}’$ 证明我们知道 $P’$ 的开口，验证者检查 $P’\stackrel{?}=\langle\mathbf{a’},\mathsf{fold}(\mathbf{G},u^{-1})\rangle$。

但是，与其通过发送 $\mathbf{a}’$ 来证明我们知道 $P’$ 的开口，我们可以递归地应用算法，通过发送大小为 $n/4$ 的向量 $\mathbf{a}{\prime\prime}$ 来证明我们知道 $P’$ 的开口。实际上，我们可以继续递归，直到 $a^{\prime\dots\prime}$ 的大小为 $n=1$。

下面的动画提供了发生事情的直观理解。下一节将详细描述动画。

为了使这个算法起作用，向量的长度必须是 2 的幂。然而，如果长度不是 2 的幂，我们可以用零填充向量，直到长度为 2 的幂。

以 $\mathcal{O}(\log n)$ 数据证明我们知道 $P$ 的开口

算法

证明者和验证者同意一个长度为 $n$ 的基向量 $\mathbf{G}$。证明者向验证者发送 $P$，即 $\langle\mathbf{a},\mathbf{G}\rangle$。证明者希望在只发送对数大小的数据的情况下说服验证者他们知道 $P$ 的开口。

证明者和验证者然后进行如下的算法。| 后面的参数简单来说只有证明者知道。

在下面的算法描述中，$n$ 是输入向量的长度，这些向量的长度都是一样的。

$$\ {prove_commitments_{log}}(P, \mathbf{G}, | \mathbf{a})$$

情况 1: $n = 1$

1. 证明者发送 $a$，验证者检查 $aG \stackrel{?}= P$，算法结束。

情况 2: $n > 1$

1. 证明者计算并发送给验证者 $(L, R)$ 其中 $$ \begin{align} L &= a_1G_2 + a_3G4 + \dots a{n-1}G_n\ R &= a_2G_1 + a_4G_3 + \dots anG{n-1} \end{align} $$
2. 验证者发送随机数 $u$
3. 证明者和验证者都计算:
   $$ \begin{align} \mathbf{G}’&=\mathsf{fold}(\mathbf{G},u^{-1})\ P’ &= Lu^2+P+Ru^{-2} \end{align} $$
4. 证明者计算 $$\mathbf{a}’=\mathsf{fold}(\mathbf{a},u)$$
5. $$\ {prove_commitments_log}(P’, \mathbf{G}’, \mathbf{a}’)$$

关于算法的评论

证明者递归地证明，给定值 $P$ 和 $\mathbf{G}$，他们知道向量 $\mathbf{a}$ 使得 $P=\langle\mathbf{a},\mathbf{G}\rangle$。双方递归地折叠 $\mathbf{G}$，直到它变成一个点，而证明者递归地折叠 $\mathbf{a}$，直到它变成一个点。

证明者在每次迭代中传输常量数量的数据，并且递归最多运行 $\log n$ 次，因此证明者发送 $\mathcal{O}(\log n)$ 数据。

我们强调，这个算法不是零知识，因为在 $n=1$ 的情况下，验证者了解到整个向量。验证者也可以发送非随机值 $u$ 来尝试了解关于 $\mathbf{a}$ 的信息。

然而，回想一下，我们设计这个算法的动机是减少检查的大小 $t_u=\langle\mathbf{l}_u,\mathbf{r}_u\rangle$，而且 $\mathbf{l}_u$ 和 $\mathbf{r}_u$ 本身从一开始就是不秘密的。

实际上，我们尚未展示如何用对数大小的数据证明我们知道内积，我们仅仅展示了我们用对数大小的数据知道一个承诺的开口。然而，更新我们的算法以展示我们知道两个向量的内积是很简单的，正如我们将在本文后面做的那样。

运行时间

验证者执行计算 $\mathbf{G}’ = \mathsf{fold}(\mathbf{G}, u^{-1})$ $\log n$ 次，并且第一次 $\mathsf{fold}$ 需要 $\mathcal{O}(n)$ 的时间。乍一看，似乎验证者的运行时间是 $\mathcal{O}(n \log n)$。然而，请注意在每次迭代中，$n$ 减半，这导致运行时间为 $n + \frac{n}{2} + \frac{n}{4} + … + 1 = 2n$，最终验证者的整体运行时间为 $\mathcal{O}(n)$。

证明我们知道内积 $\langle\mathbf{a},\mathbf{b}\rangle=v$

我们现在调整上述算法，证明我们在两个标量向量之间进行了内积，而不是字段元素向量和椭圆曲线点向量之间的内积。

具体来说，我们必须证明 $P$ 保存对内积 $\langle\mathbf{a},\mathbf{b}\rangle$ 的承诺。这个内积是一个标量，因此我们需使用普通的Pedersen承诺，而不是向量承诺。为此，我们使用一个随机的椭圆曲线点（具有未知的离散对数）$Q$。因此，$P = \langle\mathbf{a},\mathbf{b}\rangle Q$。

然而，我们不能简单地重用之前的算法，因为证明者可以提供多个对 $P$ 的开口。例如，如果 $\mathbf{a} = [1,2]$ 且 $\mathbf{b} = [3,4]$...