向量承诺的简洁证明

如果我们有一个 Pedersen 向量承诺 $A$，它包含对向量 $\mathbf{a}$ 的承诺，形式为 $A = a_1G_1 + a_2G_2+\dots + a_nG_n$，我们可以通过将 $\mathbf{a}$ 发送给验证者来证明我们知道承诺的开启，验证者会检查 $A \stackrel{?}= a_1G_1 + \dots + a_nG_n$。这要求将 $n$ 个元素发送给验证者（假设 $\mathbf{a}$ 的长度为 $n$）。

在上一章中，我们展示了如何做到这一点而不泄露任何信息。本章中，我们展示了如何在发送少于 $n$ 个元素的情况下证明我们知道开启，但没有零知识属性。

动机

我们在此开发的技术将成为证明有效内积计算的重要构建块，证明的大小为 $\log n$，其中 $n$ 是向量的长度。

在上一章中，我们展示了如何证明我们正确执行内积，但不揭示向量或结果。但是，证明的大小是 $\mathcal{O}(n)$，因为证明者发送 $\mathbf{l}_u$ 和 $\mathbf{r}_u$ 的步骤。

本文中的子例程将在减少证明大小方面发挥重要作用。本文章不是关注零知识，因为前面讨论的算法具有零知识属性。也就是说，$\mathbf{l}_u$ 和 $\mathbf{r}_u$ 本身并不保密，因此无须对其进行模糊化。

问题陈述

给定一个商定的基向量 $\mathbf{G}=[G_1,\dots,G_n]$，证明者向验证者提供一个 Pedersen 向量承诺 $A$，其中 $A$ 是对 $\mathbf{a}$ 的非盲承诺，即 $A = \langle[a_1,\dots,a_n],[G_1,\dots,G_n]\rangle$，并希望证明他们知道承诺的开启，同时发送少于 $n$ 个项，即发送整个向量 $[a_1,\dots,a_n]$。

一个小于 $n$ 的证明

缩小证明大小依赖于三个见解：

见解 1：内积 $\langle \mathbf{a},\mathbf{b}\rangle$ 是外积的对角线

我们将利用的第一个见解是内积是 外积 的对角线。换句话说，外积“包含”内积。在一维向量的上下文中，外积是通过将第一个一维向量中的每个元素与第二个向量中的每个其他元素相乘而形成的二维矩阵。例如：

$$ \begin{align} \mathbf{a}=[a_1, a_2],\space \mathbf{b}=[b_1, b_2], \end{align} \space\space \mathbf{a} \otimes \mathbf{b} = \begin{pmatrix} \boxed{a_1 b_1} & a_1 b_2 \ a_2 b_1 & \boxed{a_2 b_2} \ \end{pmatrix} $$

这可能看起来像是朝错误的方向，因为外积需要 $\mathcal{O}(n^2)$ 的步骤来计算。然而，以下见解表明，有可能在 $\mathcal{O}(1)$ 的时间内间接计算外积。

见解 2：外积的和等于原始向量的和的乘积

第二个观察是外积的项的和等于原始向量和的乘积。也就是说，

$$ \sum_{i=1}^{n} ai\sum{i=1}^{n} b_i=\sum\mathbf{a} \otimes \mathbf{b} $$

对于我们向量 $[a_1,a_2]$ 和 $[b_1,b_2]$ 的例子，这将成为

$$ \underbrace{(a_1 + a_2)(b_1 + b2)}{\sum a_i\sum b_i} = \underbrace{a_1b_1 + a_1b_2 + a_2b_1 + a_2b2}{\sum\mathbf{a} \otimes \mathbf{b}} $$

从图形上看，这可以想象成矩形的面积，边长为 $(a_1 + a_2) \times (b_1 + b_2)$ 与 $a_1 \times b_1 + a_1 \times b_2 + a_2 \times b_1 + a_2 \times b_2$ 的“面积”相同。

$$ \begin{array}{|c|cc|} \hline &a_1+a_2\ \hline b_1&a_1b_1 + a_1b_2\ +b_2& + a_2b_1 + a_2b_2\ \hline \end{array}= \begin{array}{|c|c|c|} \hline &a_1&a_2\ \hline b_1&a_1b_1&a_2b_1\ \hline b_2&a_1b_2&a_2b_2\ \hline \end{array} $$

在我们的例子中，向量 $\mathbf{b}$ 实际上是椭圆曲线点的基向量，所以我们可以说

$$ (a_1 + a_2)(G_1 + G_2) = a_1G_1 + a_1G_2 + a_2G_1 + a_2G_2 $$

注意我们的原始 Pedersen 承诺

$$ A = \langle[a_1,a_2],[G_1,G_2]\rangle = a_1G_1 + a_2G_2 $$

嵌入了外积的盒装项中：

$$ (a_1 + a_2)(G_1 + G_2) = \boxed{a_1G_1} + a_1G_2 + a_2G_1 + \boxed{a_2G_2} $$

因此，通过将向量项的和相乘，我们也计算了外积的和。

由于内积是外积的对角线，因而我们已经 间接地 通过将向量项的和相乘来计算内积。为了证明我们知道内积，我们需要证明我们也知道外积中不属于内积的项。

对于长度为 2 的向量，我们可以将外积中不属于内积的部分称为 非对角线乘积。

下面，我们将用 $\square$ 标记构成非对角线乘积的项，用 $\blacksquare$ 标记构成内积的项：

$$ \begin{array}{|c|c|c|} \hline &a_1&a_2\ \hline b_1&\blacksquare&\square\ \hline b_2&\square&\blacksquare\ \hline \end{array} $$

我们现在可以正式陈述我们将依赖的关系。如果 $n=2$，则有： $$\sum\mathbf{a}\otimes\mathbf{b}=\langle\mathbf{a},\mathbf{b}\rangle+\mathsf{off\_diagonal}(\mathbf{a},\mathbf{b})$$

如果其中一个向量是椭圆曲线点的向量（即使它们的离散对数未知），该关系也成立。

对于 $n > 2$ 的情况，证明内积的知识意味着证明者需要说服验证者他们知道下面紫色阴影区域的“面积”。

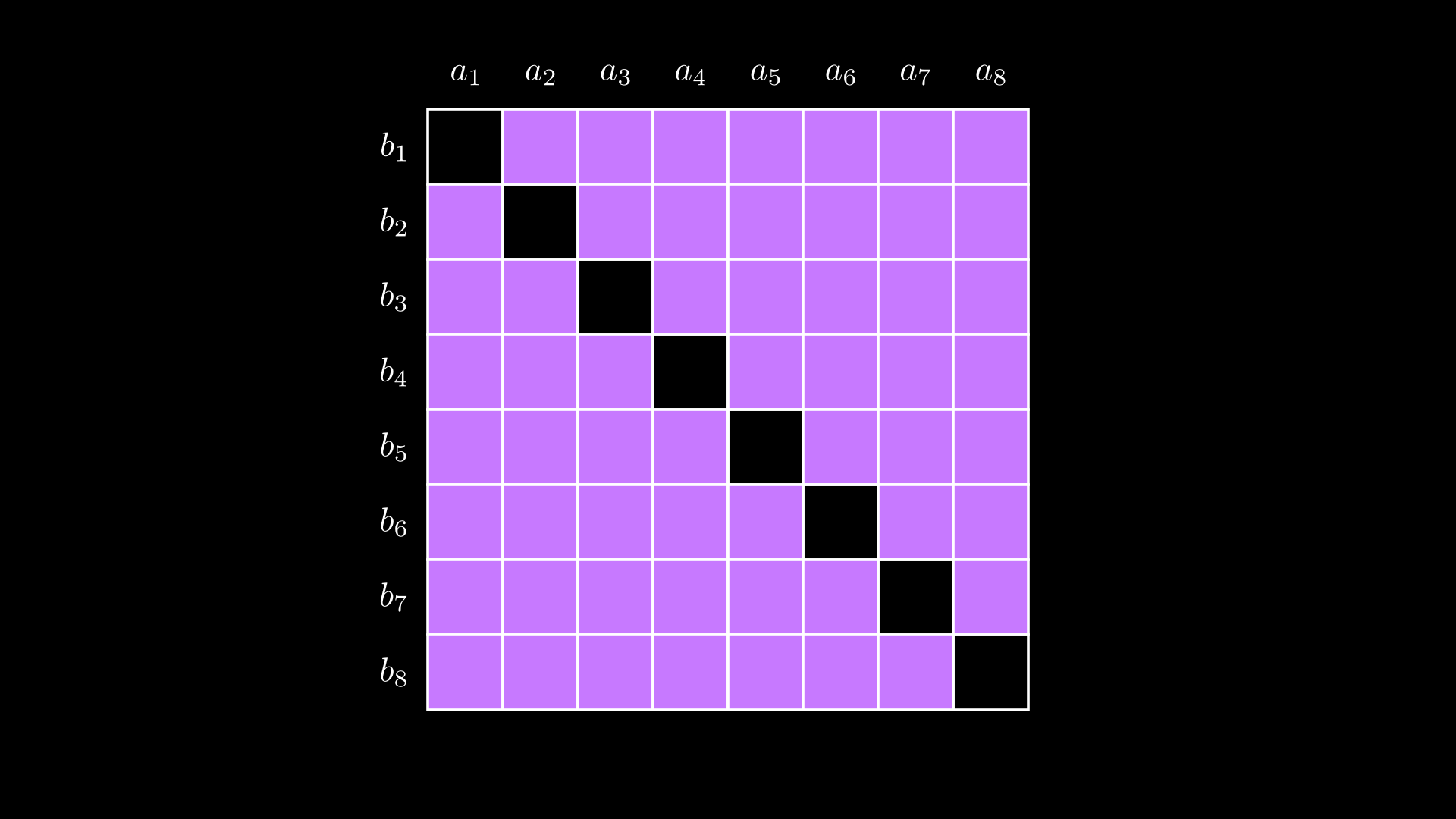
在 $n > 2$ 时简洁地传达这一信息更为棘手，因此我们稍后会重新审视这一点。

在 $n = 2$ 的情况下，面积仅仅是非对角线部分。

见解 3：如果 $n = 1$，则内积等于外积

一个重要的边缘案例是，当我们有一个长度为 1 的向量。在该情况下，证明者只需将验证者的 $\mathbf{a}$（长度为 1）发送给验证者，而验证者只需将 $\mathbf{a}$ 的单个元素与 $\mathbf{G}$ 的单个元素相乘。

算法草图

我们现在可以为案例 $n=2$ 创建一个算法的初稿，以证明我们已经计算出 $\mathbf{a}$ 和 $\mathbf{G}$ 的内积，这等价于展示我们知道承诺 $A$。

证明者与验证者之间的交互如下：

1. 证明者将他们的承诺 $A = a_1G_1 + a_2G_2$ 发送给验证者。
2. 证明者将 $\mathbf{a}$ 中的所有项相加，并将其发送为 $a’ = a_1 + a_2$ 给验证者（请注意，向量的分量求和是一个标量，因此对 $\mathbf{a}$ 的元素求和得出的标量为 $a’$）。此外，证明者计算 $\mathbf{a} \otimes \mathbf{G}$ 的非对角线项（即 $R = a_2G_1$，$L = a_1G_2$），并将 $L$ 和 $R$ 发送给验证者。

从图形上看，$L$ 和 $R$ 可以如下所示：

$$ \begin{array}{|c|c|c|} \hline &a_1&a_2\ \hline G_1&&R\ \hline G_2&L&\ \hline \end{array} $$

3. 验证者通过计算 $a’G’$ 间接计算 $\mathbf{a} \otimes \mathbf{G}$，其中 $G’ = G_1 + G_2$ 并检查

$$\underbrace{a’G’}\text{外积和} = \underbrace{A}\text{内积} + \underbrace{L + R}_\text{非对角线项}$$

在展开形式中，上述等式为： $$\underbrace{(a_1 + a_2)(G_1 + G2)}\text{外积} = \underbrace{a_1G_1 + a_2G2}\text{内积} + \underbrace{a_1G_2 + a_2G1}\text{非对角线项}$$

请注意，上述检查等价于之前的关系：

$$\sum\mathbf{a}\otimes\mathbf{G}=\langle\mathbf{a},\mathbf{G}\rangle+\mathsf{off\_diagonal}(\mathbf{a},\mathbf{G})$$

安全漏洞：多个开启

然而，有一个安全问题——证明者可能会为同一承诺找到多个证明。例如，证明者可以随机选择 $L$，然后计算

$$ R = a’G’ – L $$

为了防止这种情况，我们重用了我们讨论零知识乘法的类似思想——证明者必须在计算中包含验证者提供的随机性 $u$。他们还必须在获取 $u$ 之前 提前 发送 $L$ 和 $R$，以便 $L$ 和 $R$ 无法被“有利地”选择。

证明者必须单独发送 $L$ 和 $R$ 而非发送它们的总和 $L + R$ 的原因是，因为证明者能够在没有限制的情况下在 $L$ 和 $R$ 之间移动值。换句话说，因为

$$L + R = a’G’$$

证明者可以选择某个椭圆曲线点 $S$，并计算出虚假的 $L’$ 和 $R’$ 为

$$\underbrace{(L + S)}{L’} + \underbrace{(R – S)}{R’} = a’G’$$

我们需要强制证明者将 $L$ 和 $R$ 分开。

以下是更新后的算法，以修正这一漏洞：

1. 证明者和验证者就基向量 $[G_1, G_2]$ 达成一致，该基向量的点是随机选择的，并且它们的离散对数未知。

2. 证明者计算并发送给验证者 $(A, L, R)$： $$ \begin{align} A &= a_1G_1 + a_2G_2 && \text{// 我们正在证明其知识的向量承诺}\ L &= a_1G_2 && \text{// 左对角线项 }\ R &= a_2G_1 && \text{// 右对角线项}\ \end{align} $$

3. 验证者回复一个随机标量 $u$。

4. 证明者计算并发送 $a’$：

$$a’ = a_1 + a_2u$$

5. 现在持有 $(A, L, R, a’, u)$ 的验证者检查：

$$ L + u A + u^2R \stackrel{?}= a'(u G_1 + G_2) $$

从底层来看，这被写为： $$ \underbrace{a_1G_2}_L + \underbrace{u(a_1G_1 + a_2G2)}{uA} + \underbrace{a_2u G1}{u^2R} = \underbrace{(a_1 + u a2)}{a’}(u G_1 + G_2) $$

若证明者正确计算了 $a’$、$L$ 和 $R$，则此等式完全正确。

请注意，验证者将 $u$ 应用于 $G_2$，而证明者将 $u$ 应用于 $a_1$。这使得原始内积的项成为结果多项式的线性系数。

$L$ 和 $R$ 之间用 $u^2$ 分开，验证者控制，从而防止恶意证明者进行之前描述的攻击。换句话说，证明者不能将值从 $R$ 移动到 $L$，因为他们移动的值必须按 $u^2$ 缩放，但证明者必须在收到 $u$ 之前发送 $L$ 和 $R$。

对算法的另一种解释：将 $n$ 的维度减半

验证者只进行一次乘法，即 $a...