零知识乘法

零知识多项式乘法

使用前一章的多项式承诺方案，证明者可以展示他们拥有三个多项式 l(x)、r(x) 和 t(x)，并证明 t(x) = l(x)r(x)。

为了使这个算法有效，验证者必须相信多项式的评估是正确的——但这是我们在前一章中展示过的。在这里的大部分步骤只是重复我们之前所做的多项式承诺算法。

在高层次上，证明者承诺 l(x)、r(x) 和 t(x)，并将承诺发送给验证者。然后，验证者随机选择一个值 x 作为 u，并要求证明者在 u 处评估多项式。验证者接着检查这些评估是否正确，并且 l(x) 的评估乘以 r(x) 的评估是否等于 t(x) 的评估。

例如，假设第一个多项式是 l(x) = 2x，第二个是 r(x) = x + 1。然后 t(x) = 2x(x + 1) = 2x² + 2。验证者可以随机抽取任何 x 值，l(x)r(x) 的结果将是 t(x)。下面的图展示了验证者选择 x = 2 的一个示例：

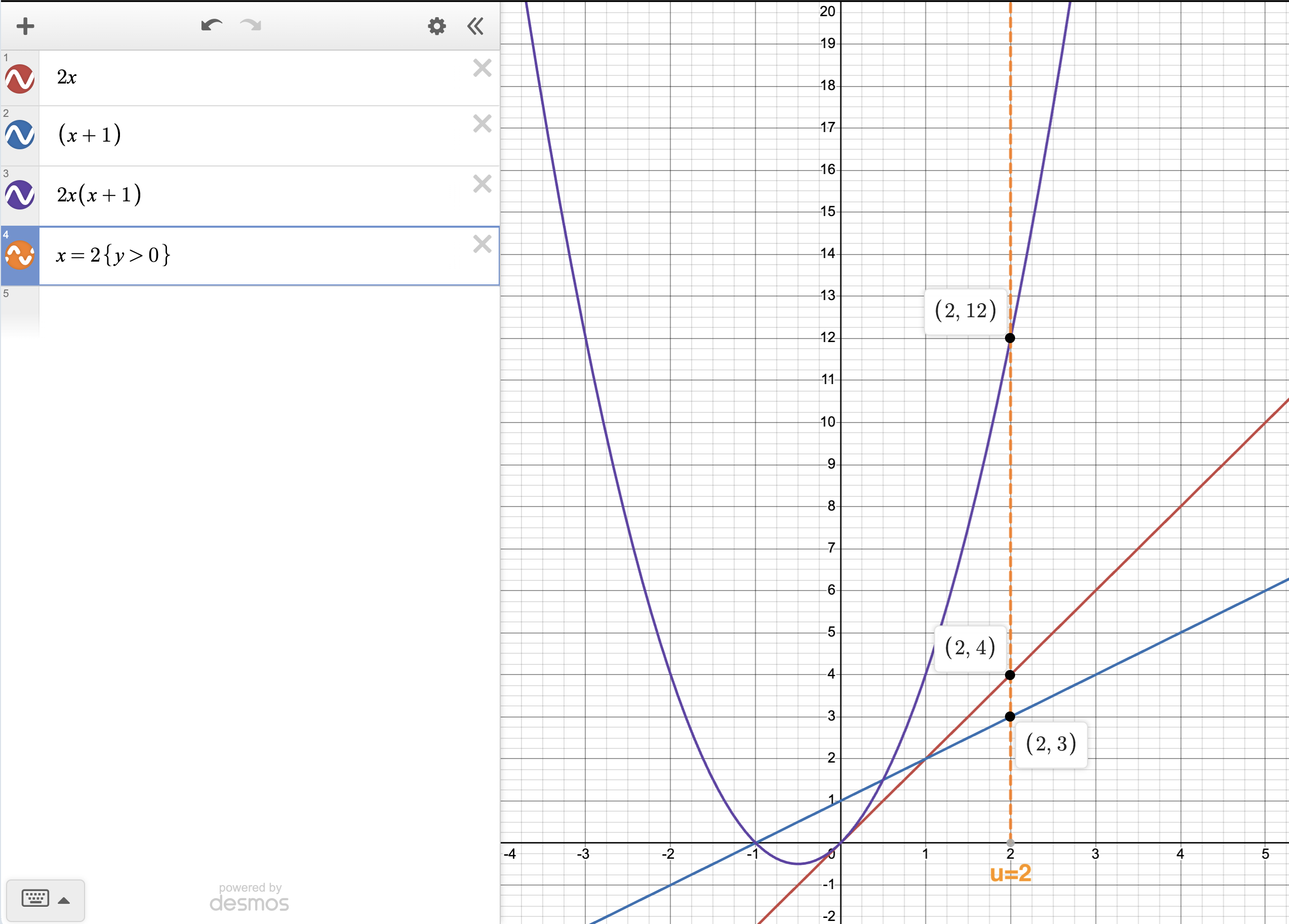
验证者接下来会检查 3×4 = 12，并接受证明者的声明。

Schwartz-Zippel 引理 表明，如果 f(x) ≠ g(x)，那么对于某个随机值 u，f(u) = g(u) 的概率小于 d/p，其中 d 是这两个多项式的最大度数，p 是有限域的阶数。如果 d ≪ p（d 远小于 p），那么 u 成为两个不相等多项式的交点的概率可以忽略不计。

具体来说，假设证明者在撒谎，l(x)r(x) ≠ t(x)。在这种情况下，考虑到极高的概率，对于随机的 u，l(u)r(u) ≠ t(u)。如果 l(x)r(x) ≠ t(x)，那么 l(x)r(x) 和 t(x) 仅在最多 d 个点相交（即 l(x)r(x) 或 t(x) 的最大度数），并且验证者随机选择的 u 是这 d 个交点之一的概率极小。

为了感受规模，d 在我们的情况下是 2，但我们的椭圆曲线（从而定义的域）的阶数约为 2^254。因此，如果 t(x) ≠ l(x)r(x)，那么 t(u) = l(u)r(u) 的概率是 1/2253，这可以忽略不计。

我们现在详细描述该算法，然后展示优化。

证明多项式乘法知识的步骤

证明者提交两个线性（1 次）多项式 l(x)、r(x) 和一个二次（2 次）多项式 t(x)，并将承诺发送给验证者。验证者回应一个随机值 u，而证明者评估 lu = l(u)、ru = r(u) 和 tu = t(u)，以及评估证明 πl、πr、πt。验证者确认所有多项式的评估都是正确的，并且 tu = l(u)r(u)。

设置

证明者和验证者就椭圆曲线点 G 和 B 达成一致，且存在一个未知的离散对数关系（即点是随机选择的）。

证明者承诺 l(x)、r(x) 和 t(x)

证明者创建三个多项式：

$$ \begin{align} l(x) &= a + s_Lx \ r(x) &= b + s_Rx \ t(x) &= l(x)r(x) = (a + s_Lx)(b + s_Rx) = ab+(as_R+bs_L)x+s_Ls_Rx^2\ \end{align} $$

因此，他们需要为每个系数生成总共 7 个 Pedersen 承诺，这将需要七个盲项 α0, α1, β0, β1, τ0, τ1, τ2

$$ \begin{align} L_0&=aG + \alpha_0B &&\text{// l(x) 的常数项 }\ L_1&=s_LG + \alpha_1B &&\text{// l(x) 线性项 }\ \ R_0&=bG + \beta_0B &&\text{// constant coefficient of }r(x)\ R_1&=s_RG + \beta_1B &&\text{// linear coefficient of }r(x)\ \ T_0 &= abG + \tau_0 B &&\text{// constant coefficient of }t(x)\ T_1 &=(as_R + bs_L)G + \tau_1B &&\text{// linear coefficient of }t(x)\ T_2 &= s_Ls_RG + \tau_2B &&\text{// quadratic coefficient of }t(x) \end{align} $$

证明者将 $(L0, L1, R0, R1, T0, T1, T2)$ 发送给验证者。

验证者生成随机标量 u

…并将域元素 u 发送给证明者。

证明者评估三个多项式并创建三个证明

证明者将 u 代入多项式，并计算在应用 u 时多项式系数承诺盲项的和。

$$ \begin{align} l_u &= a + s_Lu\ r_u &= b + s_Ru\ t_u &= ab + (as_R + bs_l)u + s_Ls_Ru^2\ \ \pi_l &= \alpha_0 + \alpha_1u \ \pi_r &= \beta_0 + \beta_1u \ \pi_t &= \tau_0 + \tau_1u + \tau_2u^2 \end{align} $$

证明者将值 $(lu, ru, tu, πl, πr, πt) $ 发送给验证者。注意这些都是域元素，而不是椭圆曲线点。

最终验证步骤

验证者检查每个多项式是否被正确评估，以及 t(u) 的评估是否是 l(u) 和 r(u) 评估的乘积。前三个检查是证明多项式相对于系数承诺被正确评估，最后一个检查验证多项式的输出是否如所声称的那样具有乘积关系。

$$ \begin{align} l_uG + \pi_l B &\stackrel{?}= L_0+L_1u &&\text{// Check that }l(u) \text{ was evaluated correctly}\ r_uG + \pi_r B &\stackrel{?}= R_0+R_1u &&\text{// Check that }r(u) \text{ was evaluated correctly}\ t_uG + \pi_t B &\stackrel{?}= T_0+T_1u+T_2u^2&&\text{// Check that }t(u) \text{ was evaluated correctly}\ t_u &\stackrel{?}= l_ur_u &&\text{// Check that }t(u)=l(u)r(u) \end{align} $$

当我们展开项时，可以看到如果证明者诚实，这些项就会平衡：

$$ \begin{align*} \underbrace{(a + sLu)}{l_u}G + \underbrace{(\alpha_0 + \alpha1u)}{\pi_l} B &\stackrel{?}= \underbrace{(aG + \alpha0B)}{L_0}+\underbrace{(s_LG + \alpha1B)}{L_1}u \ \underbrace{(b + sRu)}{r_u}G + \underbrace{(\beta_0 + \beta1u)}{\pi_r} B &\stackrel{?}= \underbrace{(bG + \beta0B)}{R_0}+\underbrace{(s_RG + \beta1B)}{R_1}u \ \underbrace{(ab + (as_R + bs_l)u + s_LsRu^2)}{t_u}G + \underbrace{...