零知识证明之书
P vs NP 及其在零知识证明中的应用
- 0xE
- 发布于 2024-10-15 10:24
- 阅读 4671
RareSkills 的 Zero Knowledge Proofs 系列文章之《P vs NP 及其在零知识证明中的应用》。
原文链接: https://www.rareskills.io/post/p-vs-np
P = NP 问题问的是:“如果我们可以快速验证一个问题的解是否正确,我们是否也能快速计算出这个解?” 大多数研究人员相信答案是否定的,即 P ≠ NP。
通过理解 P vs NP 问题,我们可以看到零知识证明(ZKP)如何融入计算机科学的更大领域,并理解 ZKP 能做什么和不能做什么。
将零知识证明与 P vs NP 问题联系起来,能够更容易地“领会”零知识证明的概念。
本教程分为三部分:
- 解释 P vs NP 问题
- 以布尔公式表达问题和解决方案
- P vs NP 及其与零知识证明的关系
前置知识
我们假设读者熟悉时间复杂度和大 $\mathcal{O}$ 符号。
如果一个算法的运行时间是 $\mathcal{O}(nᶜ)$ 或更快,我们称该算法在多项式时间内运行,其中 $n$ 是输入的大小,$c$ 是非负常数。我们可以将这些在多项式时间或更快运行的算法称为高效算法,因为它们的运行时间不会随着输入大小过快增长。
如果一个算法的运行时间是 $\mathcal{O}(cⁿ)$,我们称其为指数时间或耗时算法,其中 $c$ 是大于 1 的常数,$n$ 是输入的大小。因为随着输入大小的增加,算法的运行时间会呈指数级变慢。
第1部分:解释 P vs NP 问题
P 类问题是那些既容易解决又容易验证解是否正确的问题。
能够在多项式时间内解决,并且其解能够在多项式时间内验证的问题,被称为 P 类问题。
以下是一些计算和验证解都很容易的问题示例。这些任务可能由不同的参与者执行,一方进行计算,另一方检查结果的有效性:
P 类问题示例 1:排序列表
我们可以高效地对一个列表进行排序,也可以高效地验证列表是否已排序。
求解:对列表进行排序需要 $\mathcal{O}(n \log n)$ 时间(例如使用归并排序),这是多项式时间。虽然 $n \log n$ 不是多项式,但我们知道 $\log n < n$,因此 $(n \log n) < n²$,所以我们的算法运行时间被某个多项式限制住,满足“多项式时间”的要求。
验证:我们可以通过遍历列表并检查每个元素是否大于其左边的邻居来验证列表是否已排序,这将耗费 $\mathcal{O}(n)$ 时间。
P 类问题示例 2:返回列表中某个数字的索引(如果该数字在列表中出现)
我们可以高效地搜索一个数字是否在列表中,然后更高效地验证该数字是否存在于给定的索引位置。
求解:例如,给定列表 [8, 2, 1, 6, 7, 3],我们需要 $\mathcal{O}(n)$ 时间来确定数字 7 是否在列表中。
验证:但是,如果我们给出列表并告知 7 在索引 4 处,你可以在 $\mathcal{O}(1)$ 时间内验证该数字确实存在于该位置。如果没有给出具体位置,搜索一个元素在一般情况下需要 $\mathcal{O}(n)$ 时间,因为我们必须遍历整个列表。如果提前知道了元素的具体位置,则验证该元素确实在该位置仅需要 $\mathcal{O}(1)$ 时间。
P 类问题示例 3:判断图中两个节点是否连通
我们可以使用广度优先搜索(BFS)高效地判断图中两个节点是否连通。BFS 从一个节点开始,访问其所有邻居,排除已经访问过的节点,接着搜索这些邻居的邻居,以此类推。
求解:使用广度优先搜索发现两个节点之间的路径需要 $\mathcal{O}(n + e)$ 时间,其中 $n$ 是图中的节点数量,$e$ 是边的数量。由于边的数量 $e$ 不能超过 $n^2$,因此在最坏情况下,我们可以将 $\mathcal{O}(n + e)$ 视作 $\mathcal{O}(n²)$。
验证:我们可以在 $\mathcal{O}(n)$ 时间内验证提出的路径是否有效,只需沿着该路径检查两个节点是否真的通过该路径连通。
在以上所有示例中,求解和验证解都可以在多项式时间内完成。
作为一名密码学专家,我将为您翻译这段内容:
见证(Witness)
在计算机科学中,见证是证明你正确解决了问题的证据。在上述例子中,见证就是问题的正确答案。对于上面的例子,我们可以使用以下内容作为见证:
- 已排序的列表
- 某个数字在列表中出现的索引位置
- 图中两个节点之间的路径
我们稍后会发现,见证不一定必须是原始问题的解决方案。它也可能是同一问题的另一种表示形式的解决方案。
PSPACE 问题:并非所有问题都有可以被高效验证的解决方案
PSPACE 中的问题是指那些需要指数级资源来解决和验证的问题。之所以称它们为 PSPACE,是因为尽管它们可能需要指数级的时间来解决,但不一定需要指数级的内存空间来运行搜索。
这类问题已经被广泛研究,但至今还没有发现能够高效解决它们的算法。许多研究者认为,根本不存在解决这些问题的高效算法。如果能够发现解决这些问题的高效方法,那么也就有可能利用这种算法来破解所有现代加密系统,从而从根本上改变我们所知的计算机科学。
尽管找到这些问题的高效解决方案有着巨大的激励,但证据表明这样的解决方案可能并不存在。这些问题如此具有挑战性,以至于即使你正确地解决了它们,你也无法提供易于验证的证明(witness)。
PSPACE 问题的例子
PSPACE 例子1:找出最佳的国际象棋走法

假设我们问一台强大的计算机:"给定这个棋盘上的棋子位置,下一步最佳的走法是什么?"
计算机回答:"将f4位置的黑卒移动到f3。"
你如何相信计算机给出的答案是正确的呢?
没有高效的方法可以检查——你必须做与计算机相同的工作。这涉及对所有可能的未来棋局状态进行全面搜索。计算机无法为我们提供任何见证,使我们能够确认"将f4位置的黑卒移动到f3"确实是下一步最佳的走法。这样,这个问题的性质与我们之前讨论的例子有很大不同:我们无法高效地验证声称的最佳走法是否真的是最佳的。
在这个例子中,计算机提供的"见证"包括所有潜在的未来游戏状态。然而,这些数据的巨大体量使得高效地验证解决方案的准确性在实践中是不可能的。
PSPACE 例子2:确定正则表达式(regex)是否等价
正则表达式 a+ 和 aa* 匹配相同的字符串。如果一个字符串匹配第一个正则表达式,它也会匹配第二个,反之亦然。
然而,检查两个任意的正则表达式是否等价需要指数级的计算时间。即使一台强大的计算机告诉你它们匹配相同的字符串,计算机也无法给你一个简短的证明(witness)来证明答案是正确的。与国际象棋的例子类似,你需要搜索一个非常大的字符串空间来检查正则表达式是否等价,这将花费指数级的时间。
国际象棋和正则表达式等价性有一个共同的特征,即它们都需要指数级的资源来找到答案,也需要指数级的资源来验证答案。
比 PSPACE 更具计算密集性的问题
有些问题如此困难,以至于需要指数级的时间和指数级的内存来解决,但这些问题通常是理论性的,在现实世界中不经常出现。
这样一个问题的例子是带有"棋子永远不能移动到重现先前棋盘状态的位置"规则的跳棋游戏。为了确保在探索可能的移动空间时不重复棋盘状态,我们必须记录所有已经访问过的棋盘状态。由于游戏的长度可能是棋盘大小的指数级,因此内存需求也是指数级的。
NP问题:一些问题可以快速验证但不能快速计算
如果我们能够快速验证问题的解决方案,那么这个问题就属于 NP 类。然而,找到解决方案可能需要指数级的资源。
任何提出的解决方案(witness)可以被快速验证正确性的问题都是 NP 问题。如果这个问题也有一个在多项式时间内找到解决方案的算法,那么它就是一个 P 问题。所有的 P 问题都是 NP 问题,但极不可能所有的 NP 问题都是 P 问题。
NP 问题的例子(以下会详细解释):
- 计算数独谜题的解答 — 验证提出的数独解答。
- 计算地图的3着色(如果存在的话)— 验证提出的地图3着色方案。
- 找到使布尔公式结果为真的赋值 — 验证提出的赋值是否使公式结果为真。
注: NP 代表非确定性多项式(non-deterministic polynomial)。我们不会深入讨论这个名称的由来;我们只是给出这个名称,以免读者误以为它代表"不是多项式时间"(not polynomial time)。
NP 问题的例子
NP 例子 1:数独
在数独游戏中,玩家得到一个 9×9 的网格,其中一些数字已经填好。玩家的目标是用 1-9 的数字填满剩余的格子,使得每个数字在每行、每列和每个 3×3 的小方格中只出现一次。
给定一个数独谜题的解答,我们可以通过遍历所有列、行和 3×3 子网格来快速验证解答是否正确。这个见证可以在多项式时间内被验证。
然而,计算解答需要显著更多的资源 — 有指数级数量的组合需要搜索。对于 9×9 的网格,这对计算机来说并不困难。但是,如果我们允许数独谜题任意大:每边的大小为 n,其中 n 是 9 的倍数。在这种情况下,找到解答的难度随着 n 呈指数级增长。
NP 例子 2:地图三着色
任何二维地图的区域都可以用仅仅四种颜色"着色"(参见四色定理)。也就是说,我们可以为每个区域分配一个独特的颜色(四种颜色之一),使得没有相邻的区域共享相同的颜色。
例如,下面的图片(来自维基百科)显示了美国被涂上四种颜色:粉色、绿色、黄色和红色。请花一点时间来验证没有两个相邻的州被涂上相同的颜色:
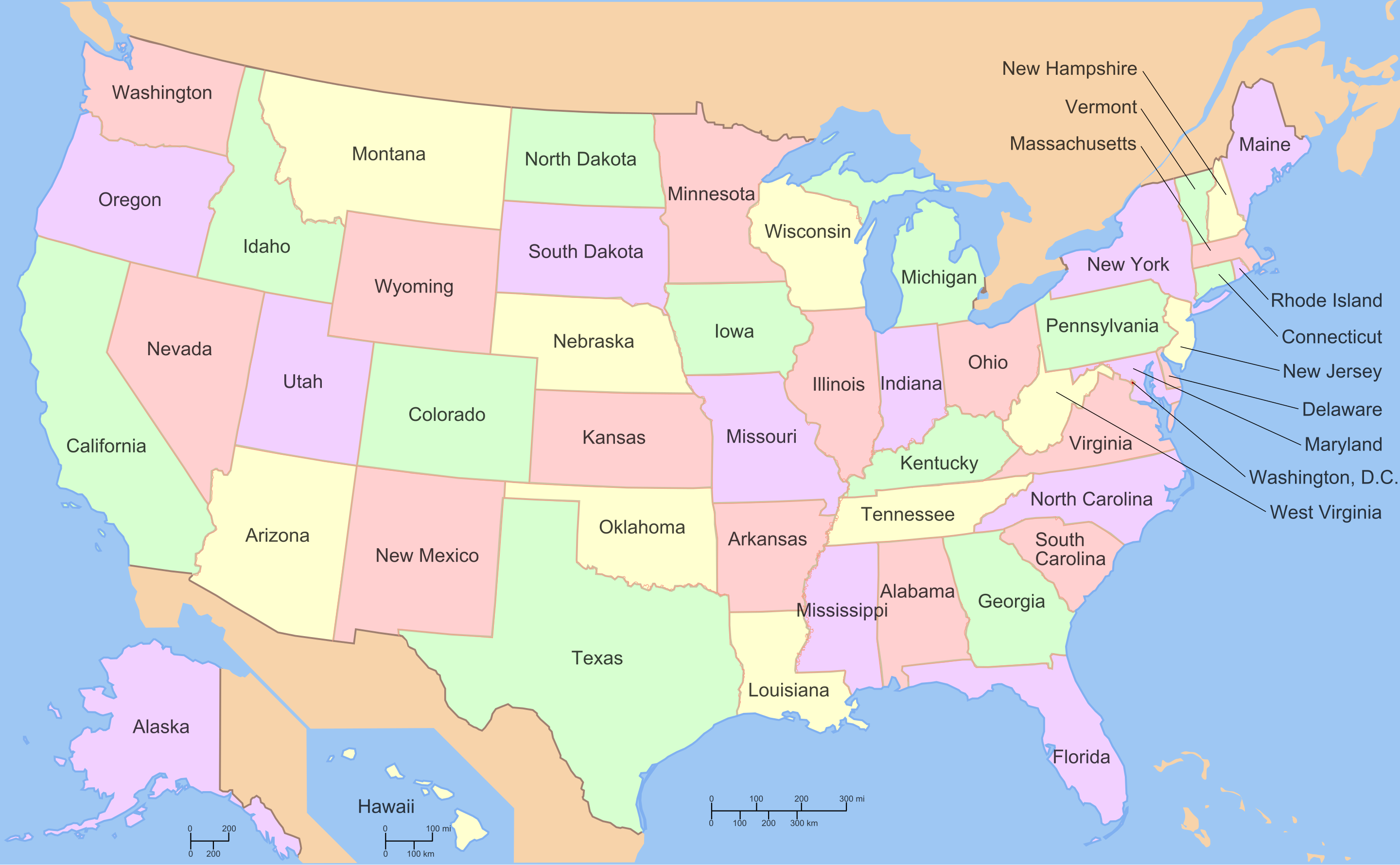
三着色问题询问是否可以仅使用三种颜色而不是四种颜色来为地图着色。发现三着色方案(如果存在的话)是一个计算密集型的搜索问题。然而,验证提出的 3 着色方案很容易:遍历每个区域,检查当前检查的区域的邻近区域是否有相同的颜色。
事实证明,美国地图是不可能 3 着色的。
某个特定地图无法用三种颜色着色的原因各不相同,但以美国为例,内华达州(下图中的红色区域)被五个领土环绕。我们给内华达州涂上一个颜色,然后必须交替涂上其邻近领土的颜色。然而,当我们完成内华达州邻居的涂色时,会发现有一个领土的边界上有三种颜色,导致无有效颜色可供未涂色的领土使用。
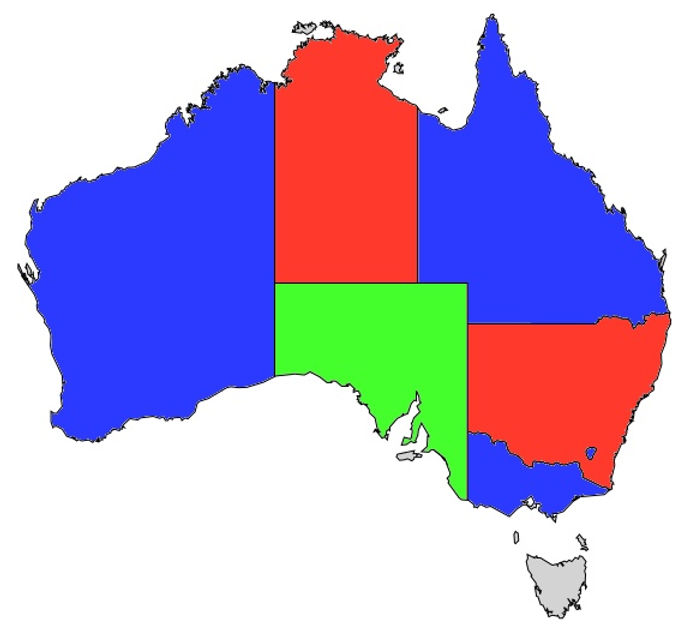
然而,澳大利亚地图是可以3着色的。
并非所有地图都可以三着色。对于任意的二维地图,如果存在三着色方案,计算这个方案是无法高效完成的 — 通常需要一个可能需要指数时间的暴力搜索。
然而,如果有人解决了三着色问题,验证他们的解决方案是很容易的。
P、NP 和 PSPACE 之间的关系
每个类别的计算资源
下表总结了每类问题所需的计算资源:
| 类别 | 计算时间 | 验证时间 |
|---|---|---|
| P | 必须是多项式时间或更好 | 必须是多项式时间或更好 |
| NP | 无要求 | 必须是多项式时间或更好 |
| PSPACE | 无要求 | 无要求 |
P、NP 和 PSPACE 之间的难度层次
任何需要指数级资源来验证见证的问题都是 PSPACE(或更难)问题。如果一个人拥有验证 PSPACE 问题见证的指数级资源,那么这个人可以轻松地计算出任何 P 或 NP 问题的解决方案。因此,所有的 P 和 NP 问题都是 PSPACE 问题的子集,如下图所示。
换句话说,如果你有一台足够强大的计算机可以解决或验证更大圆中的一类问题,你就可以解决或验证它的一个子集:
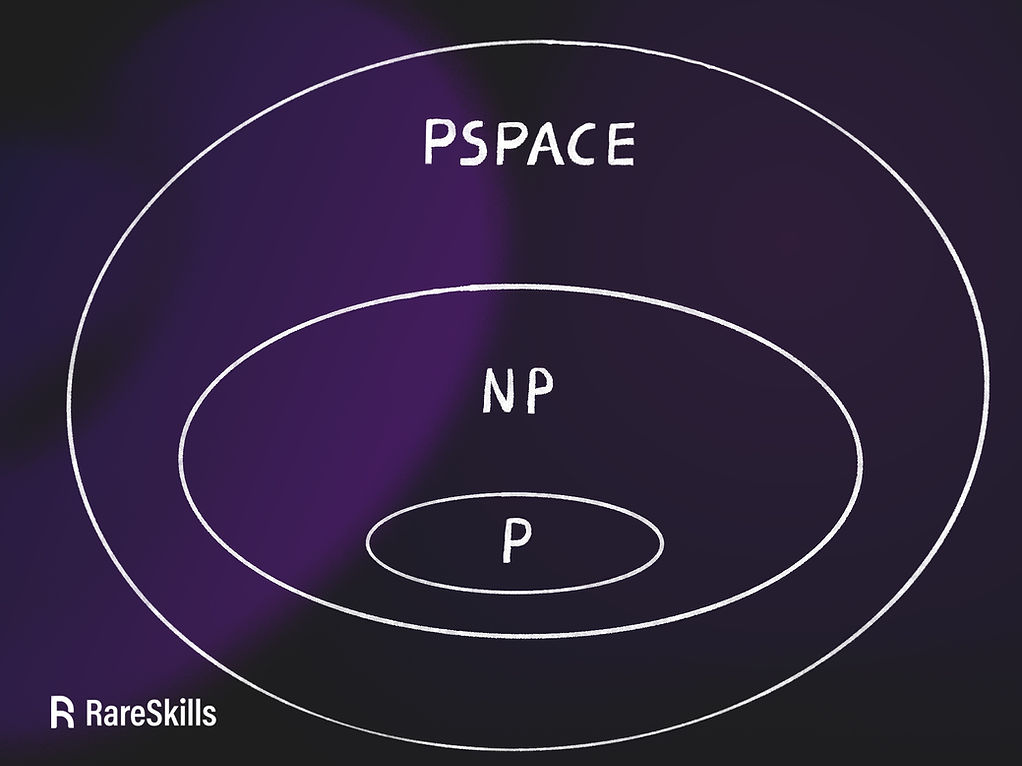
P 与 NP 问题
P 是可以被高效求解和验证的问题类别,而 NP 是可以被高效验证的问题类别。"P 与 NP"问题简单地问,这两个类别是否相同。
如果 P = NP,这意味着只要我们能找到一种高效的方法来验证解决方案,我们就也能找到一种高效的方法来找到该解决方案。请记住,找到解决方案总是至少和验证它一样困难。(根据定义,解决问题包括找到正确的答案,这意味着解决问题的算法在过程中也在验证其答案)。
如果 P = NP 成立,这意味着存在一种高效的算法来计算数独谜题(任意大小)并找出是否存在三着色。这也意味着存在一种高效的算法来破解大多数现代密码算法。
目前,P 和 NP 是否是同一个集合仍未被证明。尽管已经进行了许多尝试来为 NP 问题找到高效的算法,但所有证据都表明这样的算法不存在。
同样,PSPACE 问题是否存在高效的解决方案或验证机制仍然是一个开放问题。虽然研究人员广泛推测 P ≠ NP 且 NP ≠ PSPACE,但这些结论尚无正式的数学证明。因此,尽管做出了广泛的努力,但 NP 问题的高效解决方案和 PSPACE 问题的高效验证方法仍未被发现。
出于实际目的,我们可以假设 P ≠ NP 且 NP ≠ PSPACE。事实上,当我们将重要数据信任给现代密码学算法时,我们隐含地做出了这种假设。
第2部分:将问题和解决方案表示为布尔公式
将 P 和 NP 问题联系在一起的是它们的解决方案可以被快速验证。如果我们能够用一种通用的语言来描述所有这些(P 和 NP)问题及其解决方案,那将是极其有用的。也就是说,我们想要一种对问题的编码,这种编码可以适用于各种问题,从证明一个列表是排序的,到证明数独谜题已被解决,再到证明我们有一个三着色。
在 NP 或 P 中验证问题的解决方案可以通过验证一个布尔公式的解决方案来完成,该公式建模了这个问题。
我们所说的“建模问题的布尔公式”将在我们描述“布尔公式的解决方案”时变得清晰,并通过一些使用布尔公式建模问题的示例来说明。
布尔公式的解决方案
为了表示一个布尔公式,我们使用操作符 $¬$ 表示布尔 NOT,$∧$ 表示布尔 AND,$∨$ 表示布尔 OR。例如,$a ∧ b$ 当且仅当 $a$ 和 $b$ 都为真时才返回真。$a ∧ ¬b$ 当且仅当 $a$ 为真且 $b$ 为假时返回真。
假设我们有一组布尔变量 $x₁$、$x₂$、$x₃$、$x₄$ 以及一个布尔公式:
$$ out = (x₁ ∨ ¬x₂ ∨ ¬x₃) ∧ (¬x₂ ∨ x₃ ∨ x₄) ∧ (x₁ ∨ x₃ ∨ ¬x₄) ∧ (¬x₂ ∨ ¬x₃ ∨ ¬x₄) $$
问题是:我们能否找到 $x₁, x₂, x₃, x₄$ 的值,使得 $out$ 为真?对于上述公式,我们可以找到。用 $T$ 表示真,$F$ 表示假,我们可以将解决方案写为:
$$ \begin{align} x₁ = T \ x₂ = F \ x₃ = T \ x₄ = F \end{align} $$
将解决方案代入公式得到:
$$ \begin{align} x₁ &= T \ x₂ &= F \ x₃ &= T \ x₄ &= F \ out &= (x₁ ∨ ¬x₂ ∨ ¬x₃) ∧ (¬x₂ ∨ x₃ ∨ x₄) ∧ (x₁ ∨ x₃ ∨ ¬x₄) ∧ (¬x₂ ∨ ¬x₃ ∨ ¬x₄) \ out &= (T ∨ ¬F ∨ ¬T) ∧ (¬F ∨ T ∨ F) ∧ (T ∨ T ∨ ¬F) ∧ (¬F ∨ ¬T ∨ ¬F) \&= (T) ∧ (T) ∧ (T) ∧ (T) \&= T \ \end{align} $$
这个结果很容易验证,但对于一个非常大的布尔公式,发现解决方案可能需要指数时间。找到布尔公式的解决方案本身就是一个 NP 问题——它可能需要指数资源来找到解决方案,但验证它可以在多项式时间内完成。
但是我们必须强调:我们使用布尔公式并不是为了求解它们——而只是为了验证提出的解决方案。
所有 P 和 NP 中的问题都可以通过将它们转换为布尔公式并展示公式的解决方案来验证
在以下示例中,输入是一个 P 或 NP 问题,输出是一个布尔公式。如果我们知道原问题的解决方案,那么我们也将知道布尔公式的解决方案。
我们的目的是展示我们知道原问题的证据——但以布尔形式呈现。
示例 1:使用布尔公式检查列表是否排序
考虑一位二进制数字 $A$ 和 $B$。以下真值表在 $A > B$ 时返回真:
| A | B | A > B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
对于列 $A > B$ 可以用表达式 $A \wedge \neg B$ 建模,它只在 $A > B$ 为 1 的那一行返回 true。
现在考虑一个表达 $A = B$ 的表格:
| A | B | A = B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
那么列 $A = B$ 可以用表达式 $(A \wedge B) \vee \neg(A \vee B)$ 建模。$(A \wedge B)$在$A = 1$且$B = 1$时返回true,而$\neg(A \vee B)$在$A$和$B$都为零时返回true。
1 bit 数的表达式:
$$ \begin{align} A > B &\rightarrow A \wedge \neg B \ A = B &\rightarrow (A \wedge B) \vee \neg(A \vee B) \end{align} $$
这些表达式很快就会派上用场。
现在,我们如何比较多于1 bit 的二进制数?
二进制比较:根据最重要的不同位
假设你从两个数字的最左边的最重要位(MSB)开始,向右移动到最不重要位(LSB)。在两个数字首次不同的位上:
如果 $P$ 在该位的值为 $1$,而 $Q$ 的值为 $0$,则 $P ≥ Q$。以下动画演示了算法检测到 $P ≥ Q$ 的过程:

如果 $P = Q$,那么所有的位都是相等的。$P = Q$ 意味着 $P ≥ Q$ 也为真:

如果 $P < Q$,那么我们将在第一个 Q 为 1 而 P 为 0 的位上检测到这一点。

假设,不失一般性,我们将 $P$ 的位标记为 $p₄, p₃, p₂, p₁$,将 $Q$ 的位标记为 $q₄, q₃, q₂, q₁$。
如果 $P ≥ Q$,那么以下任一条件必须为真:
- $p₄ > q₄$
- $p₄ = q₄$ 且 $p₃ > q₃$
- $p₄ = q₄$ 且 $p₃ = q₃$ 且 $p₂ > q₂$
- $p₄ = q₄$ 且 $p₃ = q₃$ 且 $p₂ = q₂$ 且 $(p₁ > q₁ \text{ 或 } p₁ = q₁)$
我们可以将这些要点组合成一个单一的等式:
$$ \begin{align} &((p₄ > q₄)) ∨ \ &((p₄ = q₄) ∧ (p₃ > q₃)) ∨ \ &((p₄ = q₄) ∧ (p₃ = q₃) ∧ (p₂ > q₂)) ∨ \ &((p₄ = q₄) ∧ (p₃ = q₃) ∧ (p₂ = q₂) ∧ ((p₁ > q₁) ∨ (p₁ = q₁))) \end{align} $$
回想一下我们建模单个位相等和比较的布尔表达式:
$$ \begin{align} A > B &== A ∧ ¬B\ A = B &== (A ∧ B) ∨ ¬(A ∨ B) \end{align} $$
我们可以将 $A > B$ 和 $A = B$ 的表达式代入上述等式中。为了避免出现数学的“墙”,我们在下面以视频形式展示这些运算:
https://video.wixstatic.com/video/935a00_655f627a117f46ecb0a48deb2640b9a1/1080p/mp4/file.mp4
最终表示 $P ≥ Q$ 的 4 位布尔公式为:
$$ \begin{align} &(p₄ ∧ ¬q₄) ∨ \ &(((p₄ ∧ q₄) ∨ ¬(p₄ ∨ q₄)) ∧ (p₃ ∧ ¬q₃)) ∨ \ &(((p₄ ∧ q₄) ∨ ¬(p₄ ∨ q₄)) ∧ ((p₃ ∧ q₃) ∨ ¬(p₃ ∨ q₃)) ∧ (p₂ ∧ ¬q₂)) ∨ \ &(((p₄ ∧ q₄) ∨ ¬(p₄ ∨ q₄)) ∧ ((p₃ ∧ q₃) ∨ ¬(p₃ ∨ q₃)) ∧ ((p₂ ∧ q₂) ∨ ¬(p₂ ∨ q₂)) ∧ ((p₁ ∧ ¬q₁) ∨ ((p₁ ∧ q₁) ∨ ¬(p₁ ∨ q₁)))) \end{align} $$
我们称这种比较两个二进制数的布尔表达式为“比较表达式”。
检查列表是否排序
给定一个用于比较固定大小数字的布尔公式,我们可以对列表中每一对相邻元素反复应用该比较表达式,并通过 AND 操作将所有比较表达式结合起来。当且仅当所有比较表达式的 AND 结果为真时,列表才是排序的。
因此,我们可以看到,证明列表排序的见证(witness)并不一定是排序后的列表。它也可以是我们上述创建的布尔公式的输入,该输入会导致公式返回 true。
示例 2:将三着色问题表示为布尔公式
让我们再次看一下澳大利亚的地图:
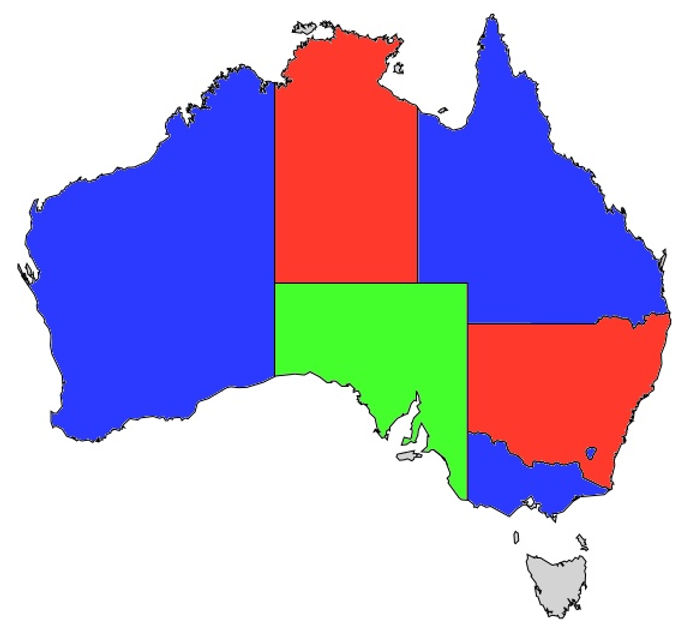
要将解决方案建模为布尔公式,该公式需要编码以下事实:
- 每个区域都有三种颜色之一。
- 每个区域的颜色与其相邻区域不同。
例如,要表示西澳大利亚州要么是绿色、蓝色或红色,我们需要创建三个变量:WESTERN_AUSTRALIA_GREEN,WESTERN_AUSTRALIA_BLUE 和 WESTERN_AUSTRALIA_RED。为了简化变量名称,我们将其简写为 WA_G、WA_B 和 WA_R。我们的布尔公式为:
$$ (\textcolor{green}{WA_G} \land \neg WA_B \land \neg WA_R) \lor (\neg {WA_G} \land \textcolor{blue}{WA_B} \land \neg WA_R) \lor (\neg {WA_G} \land \neg WA_B \land \textcolor{red}{WA_R}) $$
换句话说:
- “(西澳大利亚是绿色 且 西澳大利亚不是蓝色 且 西澳大利亚不是红色)
或
- (西澳大利亚不是绿色 且 西澳大利亚是蓝色 且 西澳大利亚不是红色)
或
- (西澳大利亚不是绿色 且 西澳大利亚不是蓝色 且 西澳大利亚是红色)”
我们称上面的公式为颜色分配约束。
我们使用布尔变量来编码一个区域的颜色分配。由于布尔变量只能有两个值,而一个区域可以有三种颜色,每个区域被分配了三个布尔变量,每个变量代表一种颜色。如果一个区域被分配了某一种颜色,那么相应的变量将被设置为“真”,而其他变量则设置为“假”。
上述公式仅在西澳大利亚被分配了恰好一种颜色时才为真。
相邻区域颜色约束
接下来,我们要编写一个公式来表达西澳与其相邻区域的颜色不同。我们像对西澳一样为南澳(South Australia,SA)创建三个变量。现在,我们的公式简单地表达为:“对于每一种颜色,西澳和南澳都不能是同一种颜色”。等价地,这意味着“西澳和南澳的颜色不同”。我们使用变量 SA_G、SA_B 和 SA_R 来表示南澳的颜色分配。我们可以使用以下公式表示它们的颜色不同:
$$\textcolor{green}{\lnot (WA_G \land SA_G)} \land \textcolor{blue}{\lnot (WA_B \land SA_B)} \land \textcolor{red}{\lnot (WA_R \land SA_R)} $$
换句话说:
- (西澳是绿色 且 南澳是绿色) 的情况不成立
且
- (西澳是蓝色 且 南澳是蓝色) 的情况不成立
且
- (西澳是红色 且 南澳是红色) 的情况不成立
这个公式成立当且仅当西澳和南澳没有被分配相同的颜色。我们将上述公式称为边界约束。
我们需要将颜色分配约束应用于每个区域,将不同颜色约束应用于每对相邻区域,然后通过 AND 操作将所有约束结合起来。
建模澳大利亚的三着色问题的公式
现在我们展示验证澳大利亚有效三着色的最终布尔公式。首先,我们为每个区域分配一个变量名:
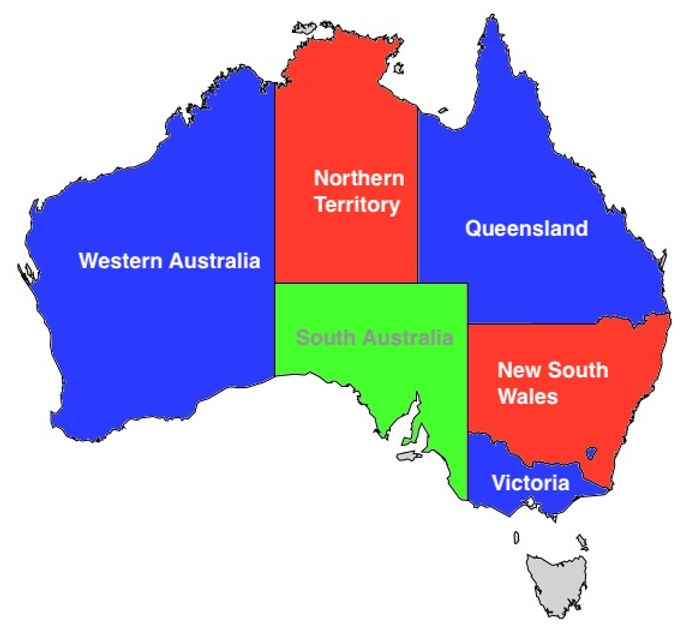
- WA = 西澳大利亚(Western Australia)
- SA = 南澳大利亚(South Australia)
- NT = 北领地(Northern Territory)
- Q = 昆士兰(Queensland)
- NSW = 新南威尔士(New South Wales)
- V = 维多利亚(Victoria)
颜色约束:每个六个领土中恰好有一种颜色:
$$ \textcolor{green}{(WA_G} \land \neg {WA_B} \land \neg {WA_R}) \lor (\neg {WA_G} \land \textcolor{blue}{WA_B} \land \neg {WA_R}) \lor (\neg {WA_G} \land \neg{WA_B} \land \textcolor{red}{WA_R}) $$
$$ \textcolor{green}{(SA_G} \land \neg {SA_B} \land \neg {SA_R}) \lor (\neg {SA_G} \land \textcolor{blue}{SA_B} \land \neg {SA_R}) \lor (\neg {SA_G} \land \neg {SA_B} \land \textcolor{red}{SA_R}) $$
$$ \textcolor{green}{(NT_G} \land \neg {NT_B} \land \neg {NT_R}) \lor (\neg {NT_G} \land \textcolor{blue}{NT_B} \land \neg {NT_R}) \lor (\neg {NT_G} \land \neg {NT_B} \land \textcolor{red}{NT_R}) $$
$$ \textcolor{green}{(Q_G} \land \neg {Q_B} \land \neg {Q_R}) \lor (\neg {Q_G} \land \textcolor{blue}{Q_B} \land \neg {Q_R}) \lor (\neg {Q_G} \land \neg {Q_B} \land \textcolor{red}{Q_R}) $$
$$ \textcolor{green}{(NSW_G} \land \neg {NSW_B} \land \neg {NSW_R}) \lor (\neg {NSW_G} \land \textcolor{blue}{NSW_B} \land \neg {NSW_R}) \lor (\neg {NSW_G} \land \neg {NSW_B} \land \textcolor{red}{NSW_R}) $$
$$ \textcolor{green}{(V_G} \land \neg {V_B} \land \neg {V_R}) \lor (\neg {V_G} \land \textcolor{blue}{V_B} \land \neg {V_R}) \lor (\neg {V_G} \land \neg {V_B} \land \textcolor{red}{V_R}) $$
边界约束:相邻的领地不共享相同的颜色
接下来,我们遍历边界,并为相邻的领地计算一个边界约束。下面的视频展示了该算法的运行过程。我们在视频后展示边界条件的最终公式集:
https://video.wixstatic.com/video/935a00_d942bd31ee0d4e0087a0c3fe5ec8b75a/1080p/mp4/file.mp4
Western Australia 与 South Australia: $$ \neg (\textcolor{green}{WA_G} \land \textcolor{green}{SA_G}) \land \neg (\textcolor{blue}{WA_B} \land \textcolor{blue}{SA_B}) \land \neg (\textcolor{red}{WA_R} \land \textcolor{red}{SA_R}) $$
Western Australia 与 Northern Territory: $$ \neg (\textcolor{green}{WA_G} \land \textcolor{green}{NT_G}) \land \neg (\textcolor{blue}{WA_B} \land \textcolor{blue}{NT_B}) \land \neg (\textcolor{red}{WA_R} \land \textcolor{red}{NT_R}) $$
Northern Territory 与 South Australia: $$ \neg (\textcolor{green}{NT_G} \land \textcolor{green}{SA_G}) \land \neg (\textcolor{blue}{NT_B} \land \textcolor{blue}{SA_B}) \land \neg (\textcolor{red}{NT_R} \land \textcolor{red}{SA_R}) $$
Northern Territory 与 Queensland: $$ \neg (\textcolor{green}{NT_G} \land \textcolor{green}{Q_G}) \land \neg (\textcolor{blue}{NT_B} \land \textcolor{blue}{Q_B}) \land \neg (\textcolor{red}{NT_R} \land \textcolor{red}{Q_R}) $$
South Australia 与 Queensland: $$ \neg (\textcolor{green}{SA_G} \land \textcolor{green}{Q_G}) \land \neg (\textcolor{blue}{SA_B} \land \textcolor{blue}{Q_B}) \land \neg (\textcolor{red}{SA_R} \land \textcolor{red}{Q_R}) $$
South Australia 与 New South Wales: $$ \neg (\textcolor{green}{SA_G} \land \textcolor{green}{NSW_G}) \land \neg (\textcolor{blue}{SA_B} \land \textcolor{blue}{NSW_B}) \land \neg (\textcolor{red}{SA_R} \land \textcolor{red}{NSW_R}) $$
South Australia 与 Victoria: $$ \neg (\textcolor{green}{SA_G} \land \textcolor{green}{V_G}) \land \neg (\textcolor{blue}{SA_B} \land \textcolor{blue}{V_B}) \land \neg (\textcolor{red}{SA_R} \land \textcolor{red}{V_R}) $$
Queensland 与 New South Wales: $$ \neg (\textcolor{green}{Q_G} \land \textcolor{green}{NSW_G}) \land \neg (\textcolor{blue}{Q_B} \land \textcolor{blue}{NSW_B}) \land \neg (\textcolor{red}{Q_R} \land \textcolor{red}{NSW_R}) $$
New South Wales 与 Victoria: $$ \neg (\textcolor{green}{NSW_G} \land \textcolor{green}{V_G}) \land \neg (\textcolor{blue}{NSW_B} \land \textcolor{blue}{V_B}) \land \neg (\textcolor{red}{NSW_R} \land \textcolor{red}{V_R}) $$
我们通过对上述 15 个公式取布尔与(Boolean AND)来创建一个布尔公式。找到一个能使该布尔表达式结果为真的变量赋值,等价于找到一个有效的澳大利亚三色着色方案。
换句话说,如果我们知道一个有效的澳大利亚三色着色方案,那么我们也就知道如何为上述布尔公式进行正确的变量赋值。
布尔公式必须在多项式时间内构造
构造这个三色着色问题的布尔公式所需的步骤必须是多项式的。具体来说,我们需要:
- 每个区域有 3 个颜色约束
- 每个区域最多有 N 个邻接区域的颜色约束
要求构造布尔公式的步骤必须在多项式时间内完成。如果需要指数级的步骤,那么布尔公式的规模将呈指数级增长,见证(witness)的大小也会呈指数级增长——无法在多项式时间内验证。
使用布尔表达式建模问题及提出的解决方案总结
所有的P类问题和NP类问题都可以表示为一个布尔公式,该公式在我们知道对应的变量赋值(证明者)时输出“真”,这个变量赋值编码了原问题的正确解决方案。
既然我们有了一种高效展示问题解决方案的标准语言,我们就离找到一种标准方法更近了一步,这种方法可以展示我们已经解决了问题,而无需暴露具体的解决方案,即零知识证明(Zero Knowledge Proofs)。
第3部分:P vs NP 和零知识证明(ZK Proofs)
P = NP 与零知识证明的关系
零知识证明中的“知识”指的是证明者对见证(witness)的了解。
零知识证明关注的是计算的验证过程。也就是说,当你找到数独的解或地图的三色着色方案时,你能否提供某种见证(witness),使他人能够高效地验证你的解是否正确?
零知识证明的目标是证明你知道见证,但不透露该见证的具体内容。
零知识证明只适用于P类或NP类问题
零知识证明仅适用于P类或NP类问题。它们不适用于无法高效验证的问题。如果我们没有机制高效地证明正则表达式等价性,或者某一步棋是否是最优的,那么零知识证明也无法神奇地使我们提供这种高效的证明。
对于 P 类和 NP 类问题,解决方案的验证可以高效完成。零知识证明能够在隐藏计算细节的同时验证解的正确性。然而,零知识证明并不能帮助你找到数独的解或地图的三色着色方案,但它能帮助你向他人证明你确实已经找到了解。
P vs NP 与零知识证明的联系
所有可快速验证解的问题都可以转换为一个布尔公式。
能够将任意问题转换为布尔公式并不是快速找到答案的捷径。解决任意布尔表达式本身就是一个 NP 问题,找到其解可能会非常困难。
布尔公式的规模非常重要。回到象棋的例子,如果你试图用布尔公式来表示每种状态,那么公式的规模将呈指数级增长。因此,只有那些能用合理规模的布尔公式来建模的问题,才是 NP 类或 P 类问题。
在零知识证明文献中,我们通常将布尔公式称为布尔电路。
为某个问题创建零知识证明的核心是将该问题翻译成一个电路,如在证明澳大利亚三色着色或验证一个已排序列表时展示的那样。接着,你证明自己有电路的有效输入(the witness),这最终转换为零知识证明。
要构建零知识证明,必须能够高效地验证某个问题的解。必须能够构建一个布尔电路,以有效建模该解。然而,对于像确定最优象棋走法这样属于 PSPACE 类的问题,这种方法会导致电路规模呈指数级增长,使其不可行。
结论,零知识证明仅对 P 类和 NP 类问题可行,这些问题的解可以高效验证。如果无法高效验证,则无法为问题创建零知识证明。
技术细节
本文中的某些概念已被简化,以便初次接触该主题的读者理解。这里提供的信息足以解释零知识证明能做什么以及不能做什么。如果您有兴趣深入研究该主题,以下是一些澄清:
一个固定大小的棋盘($8 \times 8$)无法被分配一个难度级别,因为这个问题的难度无法表示为$\mathcal{O}(f(n))$这样的形式。严格来说,我们认为任意大小的象棋问题属于 PSPACE 类问题。虽然$10 \times 10$的棋盘可能会让人觉得复杂,但我们可以简单地规定,在起始位置时,额外的格子上没有任何棋子。
象棋有一个不太为人知的规则:如果 50 步内没有吃子或没有兵移动,玩家可以宣和。这个规则限制了搜索空间的大小,使得问题属于 PSPACE 类。如果去掉这个规则,那么这种象棋版本将属于 EXPSPACE 类问题,需要指数级的时间和内存来计算。
某些 NP 问题可以在次指数时间内解决,但从实际应用的角度来看,它们仍然需要指数时间。例如,$\mathcal{O}(2^{\sqrt{n}})$技术上属于次指数级,但解决这些问题仍然非常困难。
对于一些 NP 问题,已经有非常强大的启发式算法用于寻找解。尽管三色着色问题需要指数时间来解决,但许多实际规模合理的实例可以很快解决。例如,有200个区域的地图和有效的三色着色方案的基准问题。巧妙的算法能够在不探索指数级大搜索空间的情况下找到解。然而,对于任何旨在加速解决 NP 问题的启发式算法,总是可以设计一个特殊的实例来利用启发式算法的弱点使其无效。尽管如此,这些启发式算法对解决现实中的典型问题实例仍然非常有效。
