零知识证明之书
有限域上的椭圆曲线
- RareSkills
- 发布于 2023-09-21 21:52
- 阅读 2564
文章详细介绍了有限域上的椭圆曲线,包括它们的绘制、数学性质以及在密码学中的应用。通过多个示例和代码,展示了如何生成和操作这些曲线,并解释了其与有限域的循环群特性。
限域上的椭圆曲线是什么样子的?
可视化平滑椭圆曲线很容易,但限域上的椭圆曲线是什么样子的呢?
以下是 $y² = x³ + 3 \pmod {23}$ 的图形。
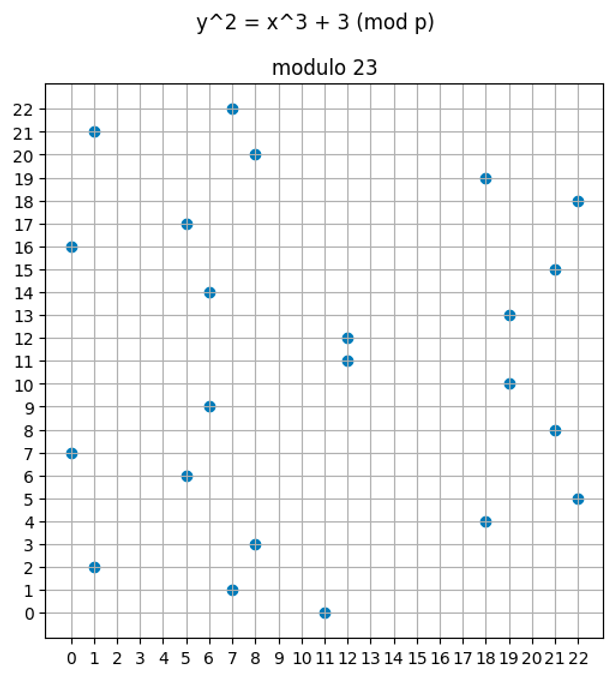
因为我们只允许整数输入(更具体地说,是有限域元素),所以我们不会获得平滑的图形。
并非每个 $x$ 值在我们解方程时都能得到一个整数 $y$ 值,因此在该值 $x$ 上不会有点。在上面的图中可以看到这样的间隙。
生成此图形的代码稍后将提供。
素数大幅改变图形
以下是关于 $y² = x³ + 3$ 在模 11、23、31 和 41 下的图形。模数越高,图形包含的点越多,图形就越复杂。
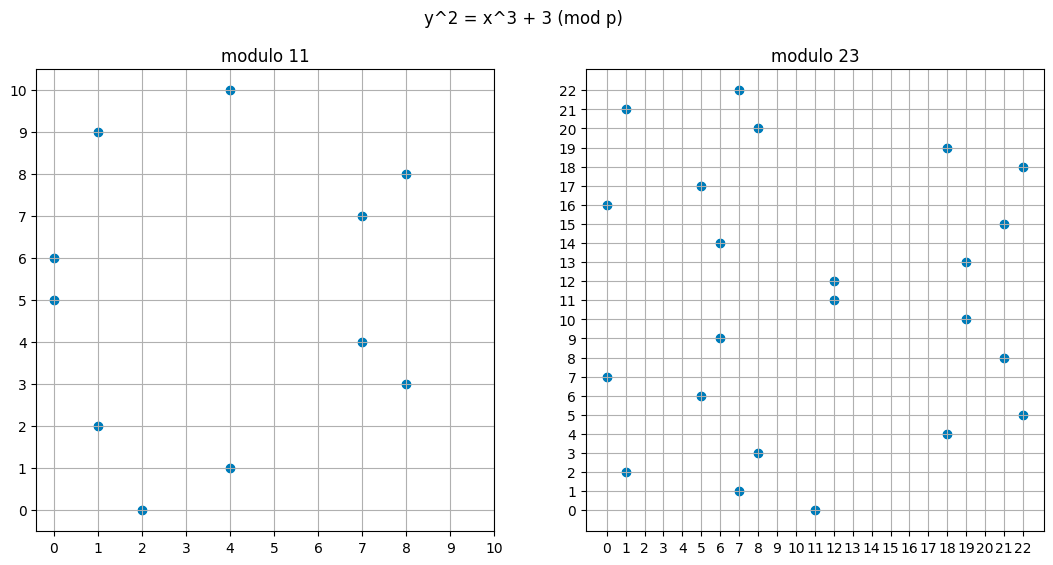
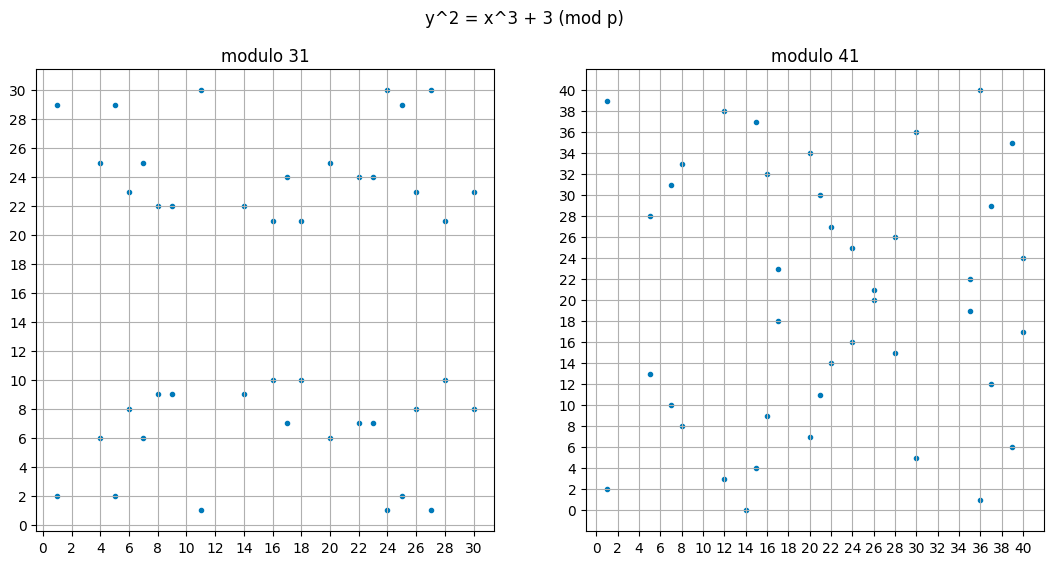
我们在上一篇文章中建立的椭圆曲线点通过“连接和翻转”操作形成一个群。当我们在一个有限域上执行这一操作时,它仍然保持为一个群,但它变成了一个循环群,这对于我们的应用非常有用。不幸的是,为什么它是循环的将需要一些非常复杂的数学,所以你现在只能接受这一点。但这应该不会太令人惊讶。我们有有限数量的点,所以通过执行 $(x + 1)G, (x + 2)G, \ldots, (x + \text{order} - 1)G$ 生成每个点至少应是合理的。
在密码学的应用中,$p$ 需要很大。在实际中,它超过 200 位。我们将在后面的部分中重新访问这一点。
背景
域元素
我们在本文中将频繁使用“域元素”这一术语,希望你已经熟悉这个术语,尤其是从我们之前的教程(特别是关于 有限域 的课程)。如果没有,它是一个在模运算内部的正整数。
也就是说,如果我们在模 11 下做加法,那么该集合中的有限域元素为 ${0, 1, \ldots, 9, 10}$。虽然我们所使用的数据类型是整数,但说“整数”并不准确。在对素数执行模加法时,不能有负的域元素(虽然整数可以是负数)。在有限域下,“负”数字仅仅是另一个数字的加法逆元,即相加后结果为零的数字。例如,在模 11 的有限域中,4 可以被视为“-7”,因为 $7 + 4 \pmod{11}$ 为 0,这在常规数字中也是 7 + (-7) 等于零的对比。
在有理数域上,乘法的身份元素是 1,而一个数字的逆是分子和分母翻转。例如,$500/303$ 是 $303/500$ 的逆,因为如果你对它们相乘,你将得到 1。
在有限域中,一个元素的逆是与之相乘以获得有限域元素 1 的数字。例如,在模 23 下,6 是 4 的逆,因为当你将它们相乘模 23 后,结果为 1。当域的阶数为素数时,每个数字(除了零)都有一个逆。
循环群
一个循环 群 是一个群,其每个元素都可以通过从生成元元素开始并反复应用该群的二元运算来计算。
一个非常简单的例子是模 11 下的整数加法。如果你的生成元是 1,并且你不断地将生成元加给自己,那么你就可以从 0 到 10 的群中生成每个元素。
说椭圆曲线点形成一个循环群(在椭圆曲线加法下)意味着我们可以将有限域中的每个数字表示为椭圆曲线点,并像在有限域中对常规整数那样相加它们。
即,
$5 + 7 \pmod p$ 与 $5G + 7G$ 是同构的。
这只适用于点数为素数的有限域上的椭圆曲线,这正是我们在实践中使用的曲线。我们将在后面再次讨论这个问题。
BN128 公式
BN128 曲线(以太坊预编译用来验证 ZK 证明)如下所示:
$$ p = 21888242871839275222246405745257275088696311157297823662689037894645226208583 $$
$$ y² = x³ + 3 \pmod p $$
这里 $p$ 是域模数。
field_modulus 不应与曲线阶数混淆,后者是曲线点的数量。
对于 bn128 曲线,曲线阶数如下:
from py_ecc.bn128 import curve_order
## 21888242871839275222246405745257275088548364400416034343698204186575808495617
print(curve_order)域模数非常大,这使得实验变得笨拙。在下一个部分中,我们将使用相同的公式,但模数较小,以培养对有限域中椭圆曲线点的直观理解。
生成椭圆曲线循环群 $y² = x³ + 3 \pmod {11}$
要解决上述方程并确定哪些 $(x, y)$ 点在曲线上,我们需要计算 $\sqrt{(x³ + 3)} \pmod{11}$。
跨模平方根
我们使用 Tonelli Shanks 公式 来计算模平方根。如果你想知道该算法如何工作,可以阅读相关资料,但现在可以将其视为一个黑盒,它计算模数上一个元素的平方根,或者告知你平方根不存在。
例如,模 11 的 5 的平方根是 4 $(4 \times 4 \mod 11 = 5)$,但模 11 的 6 没有平方根。 (鼓励读者通过暴力搜索来验证这一点)。
平方根通常有两个解,一个正解和一个负解。虽然在有限域中没有负号的数字,但我们仍然可以在逆元的意义上谈论“负数”。
你可以在网上找到实现上述算法的代码,但为了避免在本教程中放入大量代码,我们将安装一个 Python 库。
python3 -m pip install libnum安装完 libnum 后,我们可以运行以下代码来演示其用法。
from libnum import has_sqrtmod_prime_power, sqrtmod_prime_power
## 函数接受的参数# has_sqrtmod_prime_power(n, field_mod, k),其中 n**k,
## 但我们对模域中的幂没有兴趣,所以我们将 k 设置为 1
## 检查 sqrt(8) mod 11 是否存在
print(has_sqrtmod_prime_power(8, 11, 1))
## False
## 检查 sqrt(5) mod 11 是否存在
print(has_sqrtmod_prime_power(5, 11, 1))
## True
## 计算 sqrt(5) mod 11
print(list(sqrtmod_prime_power(5, 11, 1)))
## [4, 7]
assert (4 ** 2) % 11 == 5
assert (7 ** 2) % 11 == 5
## 我们预计 4 和 7 是互为反元素,因为在“常规”数学中,平方根的两个解是 sqrt 和 -sqrt。
assert (4 + 7) % 11 == 0现在我们知道如何计算模平方根,我们可以遍历 $x$ 的值并根据公式 $y² = x³ + b$ 计算 $y$。求解 $y$ 只需对两边进行模平方根(如果存在)并保存结果 $(x, y)$ 的对以便后续绘制。
让我们创建一个简单的椭圆曲线图
$$y² = x³ + 3 \pmod {11}$$
import libnum
import matplotlib.pyplot as plt
def generate_points(mod):
xs = []
ys = []
def y_squared(x):
return (x**3 + 3) % mod
for x in range(0, mod):
if libnum.has_sqrtmod_prime_power(y_squared(x), mod, 1):
square_roots = libnum.sqrtmod_prime_power(y_squared(x), mod, 1)
# 我们可能会有两个解
for sr in square_roots:
ys.append(sr)
xs.append(x)
return xs, ys
xs, ys = generate_points(11)
fig, (ax1) = plt.subplots(1, 1);
fig.suptitle('y^2 = x^3 + 3 (mod p)');
fig.set_size_inches(6, 6);
ax1.set_xticks(range(0,11));
ax1.set_yticks(range(0,11));
plt.grid()
plt.scatter(xs, ys)
plt.plot();图形结果如下所示:
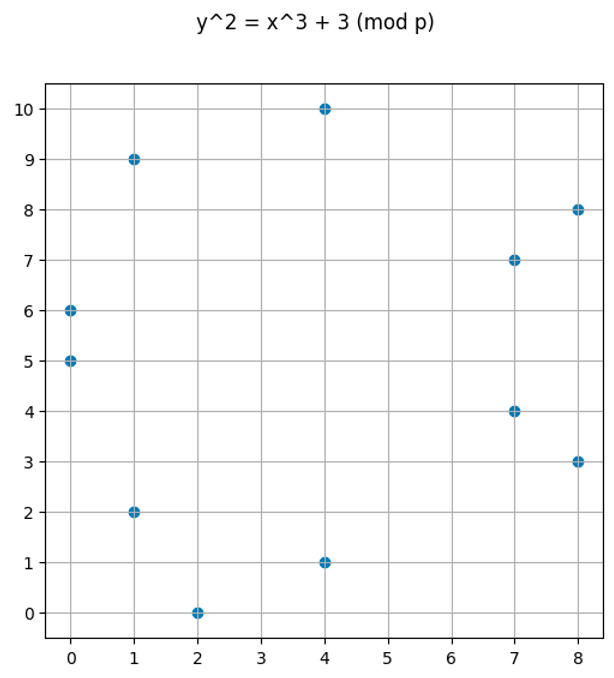
一些观察:
- 不会有任何 x 或 y 值大于或等于我们使用的模数
- 就像实值图一样,模数图“看起来是对称的”
椭圆曲线点加法
更有趣的是,我们的“连接点和翻转”操作来计算椭圆曲线仍然有效!
但是考虑到我们在有限域上执行这一步,这并不奇怪。我们在实数上的公式使用加法和乘法的正常域运算。虽然我们使用平方根来判断一个点是否在曲线上,而平方根并不是有效的域运算符,但我们并不使用平方根来计算点的加法和翻倍。
读者可以通过从上面的图中选择两个点,然后将它们插件于以下代码中来验证这一点,看看它们总是落在另一个点上(或者如果这些点互为反元素,则落在无穷点上)。这些公式取自 维基百科的椭圆曲线点乘法页面。
def double(x, y, a, p):
lambd = (((3 * x**2) % p ) * pow(2 * y, -1, p)) % p
newx = (lambd**2 - 2 * x) % p
newy = (-lambd * newx + lambd * x - y) % p
return (newx, newy)
def add_points(xq, yq, xp, yp, p, a=0):
if xq == yq == None:
return xp, yp
if xp == yp == None:
return xq, yq
assert (xq**3 + 3) % p == (yq ** 2) % p, "q不在曲线上"
assert (xp**3 + 3) % p == (yp ** 2) % p, "p不在曲线上"
if xq == xp and yq == yp:
return double(xq, yq, a, p)
elif xq == xp:
return None, None
lambd = ((yq - yp) * pow((xq - xp), -1, p) ) % p
xr = (lambd**2 - xp - xq) % p
yr = (lambd*(xp - xr) - yp) % p
return xr, yr以下是有限域中“连接与翻转”的一些可视化效果:
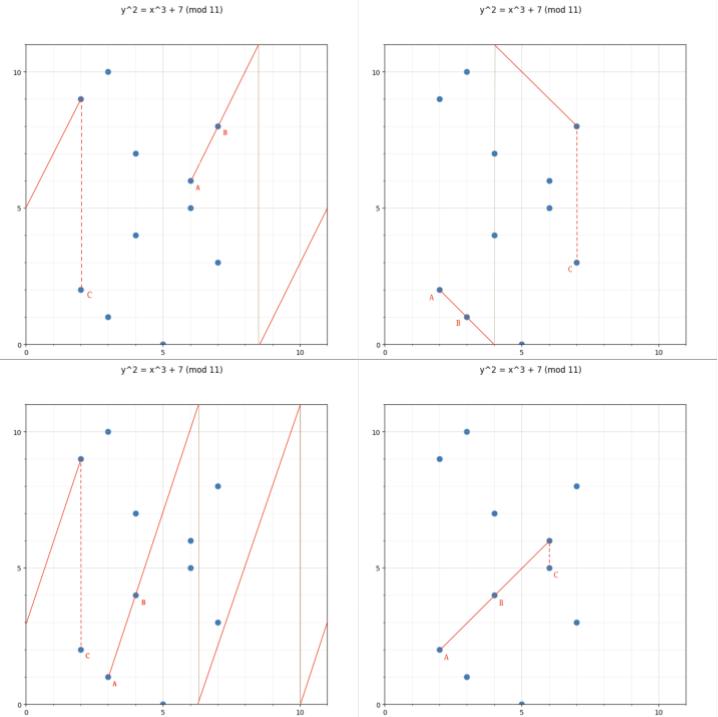
循环群中的每个椭圆曲线点都有一个“数字”
一个循环群的定义是可以通过反复将生成元相加来生成。
让我们用 $y² = x³ + 3 \pmod {11}$ 和生成点 $(4, 10)$ 来做一个实际示例。
使用上面的 Python 函数,我们可以从点 $(4, 10)$ 开始,生成群中的每个点:
## 对于我们的目的,(4, 10) 是生成点 G
next_x, next_y = 4, 10
print(1, 4, 10)
points = [(next_x, next_y)]
for i in range(2, 12):
# 反复将 G 加到下一个点以生成所有元素
next_x, next_y = add_points(next_x, next_y, 4, 10, 11)
print(i, next_x, next_y)
points.append((next_x, next_y))输出将是
0 4 10
1 7 7
2 1 9
3 0 6
4 8 8
5 2 0
6 8 3
7 0 5
8 1 2
9 7 4
10 4 1
11 None None
12 4 10 # 注意这是第一个点观察到 $(\text{order} + 1)G = G$。就像模加法一样,当我们“溢出”时,循环会重新开始。
这里 None 表示无穷远点,这确实是群的一部分。将无穷远点与生成点相加返回生成点,这就是身份元应有的行为。
我们可以为每个点分配一个“数字”,根据我们加到自身生成该点的次数。
我们可以使用以下代码来绘制曲线并在旁边标注数字。
xs11, ys11 = generate_points(11)
fig, (ax1) = plt.subplots(1, 1);
fig.suptitle('y^2 = x^3 + 3 (mod 11)');
fig.set_size_inches(13, 6);
ax1.set_title("模 11")
ax1.scatter(xs11, ys11, marker='o');
ax1.set_xticks(range(0,11));
ax1.set_yticks(range(0,11));
ax1.grid()
for i in range(0, 11):
plt.annotate(str(i+1), (points[i][0] + 0.1, points[i][1]), color="red");红色文本可以被视为从身份元开始,还有多少次我们将生成元加到自身。
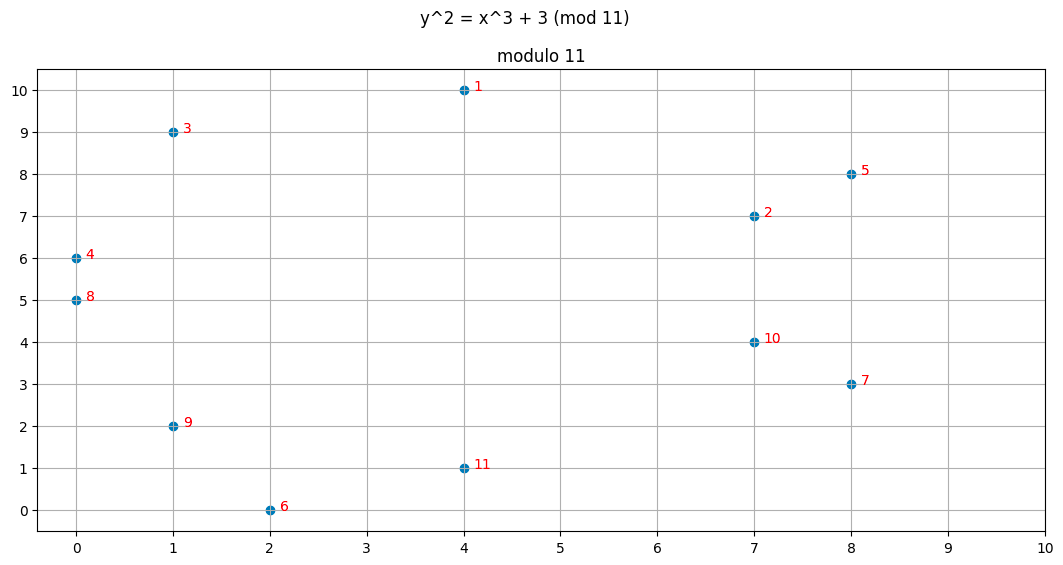
点的逆仍然是垂直对称的
有一个有趣的观察:注意那些共享相同 x 值的点相加等于 12,这对应于身份元($12 \mod 12 = 0$)。如果我们将点 $(4, 1)$(曲线图中的第 11 个点)加到 $(4, 10)$,我们将得到无穷远点,这将是群中的第 12 个元素。
阶数不是模数
在本例中,群的阶数是 12(群中椭圆曲线点的总数),尽管椭圆曲线的公式是在模 11 下。这将多次强调,但你不应假设椭圆曲线的模数是群阶。但是,你可以使用 哈斯定理 从域模数估计曲线的阶数范围。
如果点的数量是素数,则点的加法行为类似于有限域
在上图中,有 12 个点(包括 0)。在模 12 下的加法不是有限域,因为 12 不是素数。
但是,如果我们仔细选择曲线的参数,可以创建一个椭圆曲线,使得点对应于有限域中的元素。也就是说,曲线的阶等于有限域的阶。
例如,$y^2 = x^3 + 7 \pmod {43}$ 创建了一个总共有 31 个点的曲线,如下图所示:
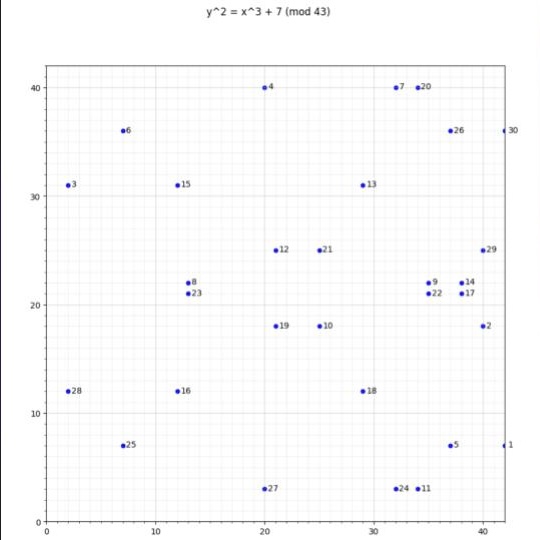
当曲线的阶与有限域的阶匹配时,你在有限域中所做的每一个操作在椭圆曲线中都有一个同构的对应。
要从有限域转换到椭圆曲线,我们选择一个点(随意)作为生成元,然后将有限域中的元素与生成元相乘。
乘法实际上是重复加法
没有椭圆曲线点的乘法。当我们说“标量乘法”时,我们实际上是指重复加法。你不能把两个椭圆曲线点相乘(虽然,通过 双线性配对,你可以做到这一点,但这是我们稍后要涉及的内容)。
当我们使用 Python 库执行 multiply(G1, x) 时,这实际上与执行 G1 + G1 + … + G1 x 次是相同的。在底层,我们实际上并不进行这么多次自加,而是使用一些聪明的技巧进行点翻倍,以在对数时间内完成操作。
例如,如果我们想计算 135G,我们实际上将高效计算以下值并缓存它们,
G, 2G, 4G, 8G, 16G, 32G, 64G, 128G…然后求和 128G + 4G + 2G + G = 135G。
当我们说 5G + 6G = 11G 时,我们实际上只是将 G 加到自身 11 次。使用上面所示的技巧,我们可以通过对数数量的计算来计算 11G,但最终,这仅仅是重复的加法。
Python bn128 库
EVM 实现 pyEVM 用于椭圆曲线预编译的库是 py_ecc,我们将大量依赖该库。下面的代码展示了生成点的样子,并演示了一些加法和标量乘法。
以下是 G1 点的样子:
from py_ecc.bn128 import G1, multiply, add, eq, neg
print(G1)
## (1, 2)
print(add(G1, G1))
## (1368015179489954701390400359078579693043519447331113978918064868415326638035, 9918110051302171585080402603319702774565515993150576347155970296011118125764)
print(multiply(G1, 2))
##(1368015179489954701390400359078579693043519447331113978918064868415326638035, 9918110051302171585080402603319702774565515993150576347155970296011118125764)
## 10G + 11G = 21G
assert eq(add(multiply(G1, 10), multiply(G1, 11)), multiply(G1, 21))尽管这些数字很大且难以阅读,但我们可以看到,将一个点自身相加的结果与将一个点“乘以”2得到的值是一样的。上面两个点显然是同一个点。元组仍然是一个 $(x, y)$ 对,只是在一个非常大的域中。
上面打印的数字很大,其原因如下。我们不希望攻击者能够从椭圆曲线点中推导出生成它的域元素。如果我们循环群的阶数太小,攻击者就可以使用暴力破解来查找。
以下是前 1000 个点的图形:
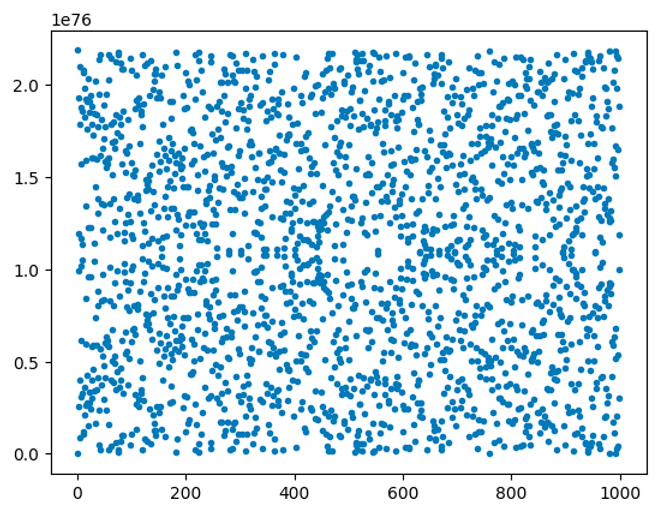
产生上图的代码如下:
import matplotlib.pyplot as plt
from py_ecc.bn128 import G1, multiply, neg
import math
import numpy as np
xs = []
ys = []
for i in range(1,1000):
xs.append(i)
ys.append(int(multiply(G1, i)[1]))
xs.append(i)
ys.append(int(neg(multiply(G1, i))[1]))
plt.scatter(xs, ys, marker='.')这可能看起来很可怕,但与我们在前面部分所做的唯一不同之处在于使用了更大的模数和不同的生成元。
库中的加法
py_ecc 库使点加法变得便利,语法应该不言而喻:
from py_ecc.bn128 import G1, multiply, add, eq
## 5 = 2 + 3
assert eq(multiply(G1, 5), add(multiply(G1, 2), multiply(G1, 3)));有限域中的加法与椭圆曲线点之间的加法是同构的(当它们的阶相等时)。由于离散对数,另一方可以在不知道生成这些点的域元素的情况下将椭圆曲线点相加。
在此时,希望读者对加法椭圆曲线点有了良好的理论和实践理解,因为现代零知识算法在这方面的依赖非常重。
关于模加法与椭圆曲线加法之间同态性的实现细节
我们在这里需要进行术语的仔细区分:
域模数是我们在曲线上进行的模运算。曲线阶是曲线上的点的数量。
如果你以某个点 $R$ 为起始点并加上曲线阶数 $o$,你将得到 $R$。如果你加上域模数,你将得到另一个不同的点。
from py_ecc.bn128 import curve_order, field_modulus, G1, multiply, eq
x = 5 # 随机选定
## 这通过
assert eq(multiply(G1, x), multiply(G1, x + curve_order))
## 这不通过
assert eq(multiply(G1, x), multiply(G1, x + field_modulus))这意味着 $(x + y) \mod \text{curve_order} == xG + yG$。
x = 2 ** 300 + 21
y = 3 ** 50 + 11
## (x + y) == xG + yG
assert eq(multiply(G1, (x + y)), add(multiply(G1, x), multiply(G1, y)))尽管 x + y 运算显然会在曲线阶数上“溢出”,但这并无所谓。就像在有限域中一样,这是我们所期望的行为。椭圆曲线乘法隐式执行与在进行乘法之前进行模运算一样的操作。
实际上,如果我们只关心正数,我们甚至不需要执行模运算,以下恒等式也保持成立:
x = 2 ** 300 + 21
y = 3 ** 50 + 11
assert eq(multiply(G1, (x + y) % curve_order), add(multiply(G1, x), multiply(G1, y)))然而,如果我们对模运算使用错误的数字(即不是曲线阶的某个数字),那么如果发生“溢出”,等式则会失效。
x = 2 ** 300 + 21
y = 3 ** 50 + 11 # 这些值足够大以至于会溢出:
assert eq(multiply(G1, (x + y) % (curve_order - 1)), add(multiply(G1, x), multiply(G1, y))), "this breaks"编码有理数
当我们进行模运算时,我们能够编码一个除法的概念。
例如,我们使用常规整数无法做到以下事情。
## 这会抛出异常
eq(add(multiply(G1, 5 / 2), multiply(G1, 1 / 2), multiply(G1, 3)然而,在有限域中,可以将 1/2 理解为 2 的乘法逆。因此,$5 / 2$ 可以被编码为 $5 \cdot \mathsf{inv}(2)$。
在 Python 中,我们可以这样做:
five_over_two = (5 * pow(2, -1, curve_order)) % curve_order
one_half = pow(2, -1, curve_order)
## 实际上 5/2 = 2.5# 2.5 + 0.5 = 3
## 但在有限域中我们这么做
assert eq(add(multiply(G1, five_over_two), multiply(G1, one_half)), multiply(G1, 3))结合律
我们知道群是结合的,因此我们期望以下人体普遍成立:
x = 5
y = 10
z = 15
lhs = add(add(multiply(G1, x), multiply(G1, y)), multiply(G1, z))
rhs = add(multiply(G1, x), add(multiply(G1...