用于零知识证明的有限域与模运算

本文是系列文章中的第三篇。我们在零知识证明的电路上下文中介绍有限域。前两篇内容为 P 变 NP 及其在零知识证明中的应用 和 算术电路。

在前一章关于算术电路的内容中，我们指出了一个局限性，即我们无法编码数字 $2/3$，因为它无法通过二进制精确表示。我们还指出，我们没有明确的方式来处理溢出。

这两个问题可以通过一种广泛应用于一般密码学的算术变体——有限域 来无缝处理。

有限域

给定一个质数 p，我们可以通过取整集合 $\set{0, 1, 2, …, p-1}$ 并定义加法和乘法进行模 $p$ 运算，来构造一个具有 p 个元素的有限域。我们将从只考虑元素个数为质数的域开始。

例如，如果质数 $p$ 为 $7$，那么有限域中的元素为 $\set{0, 1, 2, 3, 4, 5, 6}$。所有超出此范围的数字（$≥ p$ 或 $< 0$）总是被映射为这个范围内的一个“等价”数字，使用模运算。等价的技术词称为 同余。

模运算计算数字被质数除时的余数。例如，如果我们的模数是 7，那么数字 12 同余 于 5，即 $12 \pmod 7 = 5$，而数字 14 同余于 0。类似地，当我们相加两个数字，比如 3 + 5，结果 8 同余于 1（8 mod 7 = 1）。下面的动画说明了这一点：

在 Python 中，上述计算可以这样完成：

p = 7
result = (3 + 5) % p
print(result) # 输出 1

在本章中，每当我们进行计算时，我们将结果表示为范围 $0…(p-1)$ 内的数字，这是我们有限域 p 中的元素集合。例如，2 * 5 = 10，我们“简化”为 3（模 7）。

注意 3 + 5 “溢出”了 6 的限制。在有限域中，溢出并不是坏事，我们将溢出的行为定义为计算的一部分。 在模 7 的有限域中，5 + 3 被定义为 1。

下溢的处理也类似。例如，$3 - 5 = -2$，但是在模 7 中，我们得到 $5$，因为 $7 - 2 = 5$。

模算术的工作原理

在典型编程语言中，我们将有限域中的加法写作 (6 + 1) % 7 == 0，而在数学符号中，我们通常说

$$0 = 6 + 1 \pmod 7$$

或更普遍地，

$$c = a + b \pmod p$$

其中 $a$ 和 $b$ 是有限域中的数字，$c$ 是余数，它将任何数字 $≥ p$ 和 $< 0$ 映射回集合 $\set{0, 1, …, p - 1}$。

符号 $\pmod p$ 意味着所有的算术都是模 $p$ 进行的。例如，

$$a + b = c + d \pmod p$$

在 Python 或 C 中，相当于 a + b % p == c + d % p。

乘法的处理方式类似，通过将数字相乘，然后取模：

$$3 = 4 × 6 \pmod 7 = 24 \pmod 7 = 3$$

以上的乘法操作可以用两种方式可视化：

或替代方式：

我们在有限域中称一个数字为“元素”。

$p$ 和域的阶

我们用来计算模的数字称为 $p$。在我们所有的示例中，它是一个质数。在更广泛的数学领域中，$p$ 可能不一定是质数，但我们只关注 $p$ 为质数的情况。

由于这种限制，域的 阶 总是等于 $p$。阶 是域中的元素数量。我们用来计算模的数字的通用术语是域的 特征。

例如，如果我们有 $p = 5$，那么元素为 $\set{0, 1, 2, 3, 4}$。这里有 5 个元素，所以该域的阶为 5。

$p$ 的加法恒等式

任何元素加上 $p$ 都是相同的元素。例如，$(3 + 7) \pmod 7 = 3$。考虑以下动画中的示例：

加法逆元

考虑 $5 + (-5) = 0$。

在数学中，$a$ 的加法逆元是一个数字 $b$，使得 $a + b = 0$。通常，我们通过在前面放一个负号来表示加法逆元。$-a$ 是通过定义得出，其当与 $a$ 相加时结果为 $0$。

加法逆元的一般规则

• 零是它自己的加法逆元。
• 每个数字恰好有一个加法逆元。

这些加法逆元的规则也适用于有限域。尽管我们没有像 $-5$ 这样的负号元素，某些元素可以在模运算下彼此“表现”得像负数。

在常规算术中，$-5$ 是与 $5$ 相加得到 $0$ 的数字。如果我们的有限域是 $p = 7$，那么 $2$ 可以视为 $-5$ 因为 $(5 + 2) \pmod 7 = 0$。类似地，$5$ 可以视为 $-2$，因为它们是彼此的加法逆元。准确地说，$-2$ 同余于 $5$ 或 $-2 \equiv 5 \pmod 7$。

要计算一个元素的加法逆元，只需计算 $p - a$，其中 $a$ 是我们要找到该元素加法逆元的元素。例如，为了找到 14 在模 23 下的加法逆元，我们计算 $23 - 14 = 9$。我们可以看到 $14 + 9 \pmod {23} = 0$。$p$ 同余于零，所以这等同于计算 $-5$ 为 $0 - 5$。

就像实数一样：

• 有限域中的每个元素恰好有一个加法逆元。
• 零是它自己的加法逆元。

有限域中加法逆元的一般模式是，有限域前半部分的元素是后半部分元素的加法逆元，如下图所示。零是例外，因为它是其自己的加法逆元。绿色线相连的数字是有限域 $p = 7$ 中彼此的加法逆元：

练习： 假设我们选择一个 $p \geq 3$。哪些（如果有的话）非零值是自己的加法逆元？

乘法逆元

考虑 $5 × (1/5) = 1$。

$a$ 的乘法逆元是一个数字 $b$，使得 $ab = 1$。每个元素（除了零）都有一个乘法逆元。在“常规数字”中，乘法逆元为 $1 / \text{num}$。例如，5 的乘法逆元为 $1/5$，19 的乘法逆元为 $1/19$。

尽管我们在有限域中没有分数，但我们仍然可以找到相乘后“表现得像”分数的数字对。

例如，在有限域 $p = 7$ 中，4 的乘法逆元是 2，因为 $4 * 2 = 8$，而 $8 \pmod 7 = 1$。因此，2 在有限域中“表现得像” $1/4$，更准确地说，$1/4$ 同余于 $2 \pmod 7$。

有限域算术中乘法逆元的一般规则：

• 0 没有乘法逆元。
• 1 是它自己的乘法逆元。
• 每个数字（除了 0）恰好有一个乘法逆元（可能是它本身）。
• 值为 $(p - 1)$ 的元素是它自己的乘法逆元。例如，在 $p = 103$ 的有限域中，1 和 102 是它们自己的乘法逆元。在 $p = 23$ 的有限域中，1 和 22 是它们自己的乘法逆元（即将解释的原因）。另一个例子：在模 5 的有限域中，1 是自己的逆元，而 4 也是自己的逆元。$4 \times 4 = 16$，且 $16 \pmod 5 = 1$。

为什么值为 $p - 1$ 的元素是它自己的乘法逆元

当我们将 $-1$ 自己乘时，我们得到 $1$。因此，$-1$ 是实数的乘法逆元。值为 $(p - 1)$ 的元素同余于 $-1$。因此，我们期望 $(p - 1)$ 是它自己的乘法逆元，确实如此。

从另一个角度看为什么 $p - 1$ 是它自己的乘法逆元，考虑 $(p - 1)(p - 1) = p² - 2p + 1$。因为 $p$ 同余于 0，那么 $p² - 2p + 1$ 简化为 $0² - 2*0 + 1 = 1$。

有限域算术电路中的求解方案

如果我们考虑以下常规数字的算术电路，我们期望 x = -1 是唯一的满足赋值。

x * x === 1
x + 1 === 0

在一个有限域中，满足分配是同余于 $-1$ 的元素，或 $p - 1$。

使用费马小定理计算乘法逆元

费马小定理 说明

$$ a^{p}=a\pmod p, a\neq0 $$

换句话说，如果你将一个非零元素提升到 $p$，你会得到该元素。示例包括：

• $3⁵ \pmod 5 = 3$
• $4⁷ \pmod 7 = 4$
• $14⁵³ \pmod {53} = 14$

现在考虑如果我们将 $aᵖ = a \pmod p$ 的两边除以 $a$（记住，$a ≠ 0$）：

$$a^p=a$$ $$\frac{a^p}{a}=\frac{a}{a}$$ $$a^{p-1}=1$$

我们可以将结果写为

$$ a(a^{p-2}) = 1 $$

这意味着 $aᵖ⁻² \pmod p$ 是 $a$ 的乘法逆元，因为 $a$ 乘以 $aᵖ⁻²$ 的结果是 1。

一些例子：

• 在有限域 $p = 7$ 中，$3$ 的乘法逆元是 $5$，即 $3^7-2 = 5 \pmod 7$。
• 在有限域 $p = 11$ 中，8 的乘法逆元是 7，$8^{11-2} = 7 \pmod {11}$。

这种方法的优点是我们可以使用 expmod 以太坊中的预编译 来计算智能合约中的模逆元。

在实践中，这是计算乘法逆元的一个不理想方式，因为将一个数字提升到大指数是计算上昂贵的。计算乘法逆元的库在底层使用了更高效的算法。然而，当没有这样的库可用时，且你想要快速而简单的解决方案，并且计算较大指数并不过于昂贵时，费马小定理可以使用。

使用 Python 计算乘法逆元

使用 Python 3.8 或更高版本，我们可以使用 pow(a, -1, p) 来计算有限域 p 中 a 的乘法逆元。 pow 的第一个参数是底数，第二个是指数，第三个是模。

示例：

p = 17
print(pow(5, -1, p))
## 7
assert (5 * 7) % p == 1

练习： 找到模 5 下 3 的乘法逆元。还有 5 种可能性，所以尝试所有可能性，看看哪个能成功。

练习： 有限域 $p = 51$ 中 50 的乘法逆元是多少？你无需用 Python 来计算，查看“乘法逆元的一般规则”中描述的原则。

练习： 使用 Python 计算模 311 的 288 的乘法逆元。你可以通过验证 (288 * answer) % 311 == 1 来检查你的工作。

乘法逆元之和与常规分数的加法是一致的

在有限域 $p = 7$ 中，数字 2 和 4 是彼此的乘法逆元，因为 $(2 \times 4) \pmod 7 = 1$。这意味着在有限域 $p = 7$ 中，$4$ 同余于 $1/2$，而 $2$ 同余于 $1/4$。

我们说 $4$ 在有限域 $p = 7$ 中同余于 $1/2$，因为 $2 \times \mathsf{mul\_inv}(2) = 1$。$2$ 的乘法逆元是 $4$，因此我们可以将 $4$ 视为 $1/2$。

在实数中，如果我们加上 $1/2 + 1/2$，我们期望得到 $1$。在有限域中也会发生同样的事情。由于 $4$ “表现得像” $1/2$，我们期望 $4 + 4 \pmod 7 = 1$，而确实如此。

我们能够通过将数字 $5/6$ 编码为操作 $5 * (1/6)$，或 $5 \times \mathsf{mul\_inv}(6)$，在有限域中表示它。

考虑 $1/2 + 1/3 = 5/6$。如果我们的有限域是 $p = 7$，那么 $1/2$ 是 2 的乘法逆元，$1/3$ 是 3 的乘法逆元，而 $5/6$ 是 $5$ 乘以 6 的乘法逆元：

p = 7
one_half = pow(2, -1, p)
one_third = pow(3, -1, p)
five_over_six = (pow(6, -1, p) * 5) % p

assert (one_half + one_third) % p == five_over_six
## True

计算有限域中“分数”的一般方式为分子乘以分母的乘法逆元，结果模 p：

def compute_field_element_from_fraction(num, den, p):
    inv_den = pow(den, -1, p)
    return (num * inv_den) % p

当分母是 p 的倍数时，不可能这样做。例如，$1/7$ 不能在有限域 $p = 7$ 中表示，因为 pow(7, -1, 7) 没有解。模运算是在除法后取余数，$7/7$ 的余数是零，或更一般地说，当 $d$ 是 $7$ 的倍数时，$7/d$ 是零。乘法逆元意味着我们可以将一个数字与它的逆元相乘得到 1，但如果其中一个数字是零，则无法通过零乘以任何东西得到 1。

练习： 在 Python 中运行 pow(7, -1, 7)。你应该看到抛出异常 ValueError: base is not invertible for the given modulus。$7$ mod $7$ 等于零。没有任何东西可以通过零乘以得到 1。

有限域“除法”不会遭受精度损失

如果我们在大多数编程语言中除以 1 / 3，我们会遭受精度损失，因为 $0.\overline{3}$ 不能用二进制表示。

然而，在有限域中，1 / 3 只是 3 的乘法逆元。

这意味着算术电路

x + y + z === 1;
x === y;
y === z;

在有限域中有一个精确的解。如果我们使用固定点或浮点数作为算术电路的数据类型，这在可靠性方面将无法实现（考虑到 0.33333 + 0.33333 + 0.33333 的结果将是 0.99999，而不是 1）。

以下 Python 实现说明了该电路：

p = 11

## x, y, z 的值为 1/3
x = pow(3, -1, 11)
y = pow(3, -1, 11)
z = pow(3, -1, 11)

assert x == y;
assert y == z;
assert (x + y + z) % p == 1

有限域元素没有传统意义上的“偶数”或“奇数”

我们说一个数字是“偶数”，如果它能被二整除而没有余数。

在有限域中，任何元素都可以被 2 整除而没有余数。

也就是说，“除以二”实际上是乘以 2 的乘法逆元，这总会在没有“余数”的情况下导致另一个域元素。

然而，如果我们有字段元素的二进制表示，那么我们可以检查当它被转换为整数时，该元素是偶数还是奇数。如果最低有效位是 1，则该数字是奇数（如果解释为整数，而不是有限域元素）。

Python 中的有限域库

由于在 Python 中不断编写 pow 和 % p 有点繁琐，读者可能希望使用 galois 库 来替代（有限域有时称为 Galois 域，读作“加洛瓦”）。可以通过 python3 -m pip install galois 安装。

下面，我们将上一节的分数相加代码 $(1/2 + 1/3 = 5/6)$ 转换为使用 galois 库。在该库中，数学运算符被重写为在有限域中工作：

import galois
GF7 = galois.GF(7) # GF7 是一个包装 7 的类

one_half = GF7(1) / GF7(2)
one_third = GF7(1) / GF7(3)
five_over_six = GF7(5) / GF7(6)

assert one_half + one_third == five_over_six  

操作 1 / GF(a) 计算 a 的乘法逆元。

galois 库可以通过前面加负号来计算加法逆元：

negative_two = -GF(2)
assert negative_two + GF(2) == 0

分数的乘法也一致

让我们使用有限域 p = 11 来做此示例。

使用常规数字，我们知道 $1/3 * 1/2 = 1/6$。

让我们在有限域中进行同样的操作：

import galois
GF = galois.GF(11)

one_third = GF(1) / GF(3)
one_half = GF(1) / GF(2)
one_sixth = GF(1) / GF(6)

assert one_third * one_half == one_sixth

练习： 使用 galois 库检查在有限域 $p = 17$ 中 $3/4 * 1/2 = 3/8$。

非零 a, b 乘积不等于零

在有限域中，无法将两个元素相乘得到零，除非其中一个元素本身就是零。常规数字中也如此。

要理解这一点，请考虑有限域 $p = 7$。要将两个数字相乘并得到 0，则一个的项 $a$ 需要是 7 的倍数，使得 $a \pmod 7$ 为零。然而，$\set{0, 1, 2, 3, 5, 6}$ 中没有任何一个是 7 的倍数，因此这种情况不会发生。

我们将经常提到这一事实，当我们设计算术电路时。例如，如果我们知道

x₁ * x₂ * ... * xₙ ≠ 0 

那么我们可以确定所有变量 x₁, x₂, xₙ 都是不为零的——即使我们不知道它们的值。

这里是如何利用这个技巧来设计实际的算术电路。假设我们有信号 x₁, x₂, x₃。我们希望限制至少其中一个信号的值为 8，而不指定哪个信号。首先，我们计算 8 的加法逆元 a_inv(8)。于是我们可以这样表示：

(x₁ + a_inv(8))(x₂ + a_inv(8))(x₃ + a_inv(8)) === 0

这可以写成

(x₁ - 8)(x₂ - 8)(x₃ - 8) === 0

前提是 -8 是 8 在有限域的加法逆元。

只要这三个信号中的一个值为 8，那么该项将为零，整个表达式将乘积为零。这一技巧依赖于两个事实：

• 如果所有项都不为零，则没有方法使表达式评估为零。
• 8 的加法逆元是唯一的，且 8 也是 8 的加法逆元的唯一相对。换句话说，没有任何值可以使 $8 + inv(8)$ 为零。

因此，算术电路 (x₁ + a_inv(8))(x₂ + a_inv(8))(x₃ + a_inv(8)) === 0 表明至少有一个 x₁、x₂、xₙ 的值为 8。

有限域运算是结合的、交换的和分配的

就像常规数学一样，在模算术下，结合性、交换性和分配性性质成立，即

结合性

$(a + b) + c = a + (b + c) \pmod p$

交换加法

$(a + b) = (b + a) \pmod p$

交换乘法

$ab = ba \pmod p$

分配性

$a(b + c) = ab + ac \pmod p$

模平方根

在“常规数学”中，完全平方数都有整数平方根。例如，25 的平方根是 5，49 的平方根是 7，依此类推。

有限域中的元素不需要是完全平方数才能拥有平方根

考虑 $5 × 5 \pmod {11} = 3$。这意味着模 11 下，3 的平方根是 5。由于有限域的环绕性质，有限域元素不需要是完全平方数才能拥有平方根。

就像常规平方根有两个解：一个正解和一个负解，有限域中的模平方根也有两个解。唯一的例外是元素 0，只有 0 作为其平方根。

在模 11 的有限域中，以下元素具有平方根：

元素	第一个平方根	第二个平方根
0	0	不适用
1	1	10
3	5	6
4	2	9
5	4	7
9	3	8

练习： 验证表中所声称的平方根在模 11 的有限域中是否正确。

请注意，第二个平方根总是第一个平方根的加法逆元，就像实数一样。

例如：

• 在常规数学中，9 的平方根是 3 和 -3，两者互为加法逆元。
• 在模 $p = 11$ 的有限域中，9 的平方根是 3 和 8。8 是 3 的加法逆元，因为 $8 + 3 \pmod {11}$ 为 $0$，正如 $3$ 为 $-3$ 的加法逆元一样。

元素 2、6、7、8 和 10 在有限域 $p = 11$ 中没有模平方根。这可以通过将每个元素从 0 到 10（包含）求平方并观察 2、6、7、8 和 10 从未产生得出。

numbers_with_roots = set()
p = 11
for i in range(0, p):
    numbers_with_roots.add(i * i % p)

print("具有平方根的数字:", numbers_with_roots)
## 具有平方根的数字: {0, 1, 3, 4, 5, 9}

注意，3 不是一个完全平方数，但它在这个有限域中确实有平方根。

计算模平方根

模平方根可以使用 libnum 库 在 Python 中计算。下面，我们计算模 11 下 5 的平方根。函数 has_sqrtmod_prime_power 和 sqrtmod_prime_power 的第三个参数可以设置为1，以满足我们的目的。

## 使用命令 `python -m pip install libnum` 安装 libnum

from libnum import has_sqrtmod_prime_power, sqrtmod_prime_power
has_sqrtmod_prime_power(5, 11, 1) # True
list(sqrtmod_prime_power(5, 11, 1)) # [4, 7]
## 平方根通常有两个解决方案。4 和 7 是 5（模 11）的平方根

当 $p$能够表示为 $4k + 3$（$k$ 是整数）时，模平方根可以这样计算：

def mod_sqrt(x, p):
    assert (p - 3) % 4 == 0, "质数不满足 4k + 3"
    exponent = (p + 1) // 4
    return pow(x, exponent, p) # x ^ e % p

上述函数返回值 $x$ 模 $p$ 的平方根之一。另一个平方根可以通过计算返回值的加法逆元来得出。如果质数不是形如 $4k + 3$，则必须使用 托内利-香克斯算法 来计算模平方根（该算法已在上述 libnum 库中实现）。

*这意味着算术电路 `x x === y可能有两个解决方案。** 例如，在有限域p = 11中，算术电路x * x === 4看似仅接受值 2，因为 -2 不是有限域元素。然而，这种假设非常错误！值得注意的是，赋值x = 9`，它同余于 -2，也满足该电路。

练习： 使用上面的代码片段计算模 23 的有限域中的 5 的模平方根。该代码将只给你一个答案。你如何计算另一个？

有限域中的线性方程组

正如在前一章中提到的，算术电路基本上是一个方程组。有限域中的线性方程组与常规数字的线性方程组具有许多相似的性质。然而，也有一些此刻可能会出乎意料的不同之处。由于算术电路是通过有限域计算的，我们必须理解这些惊人的偏差可能出现在哪里。

线性方程组 是一组带有未知数（变量）的直线方程，我们试图同时求解它们。为了找到线性方程组的唯一解，我们必须为每个变量找到一个数值，使其能够同时满足方程组中的所有方程。

实数的线性方程组具有以下特点之一：

1. 没有解： 这意味着两个方程在二维中表示的直线是平行的，或者在三维或更高维中从不相交。

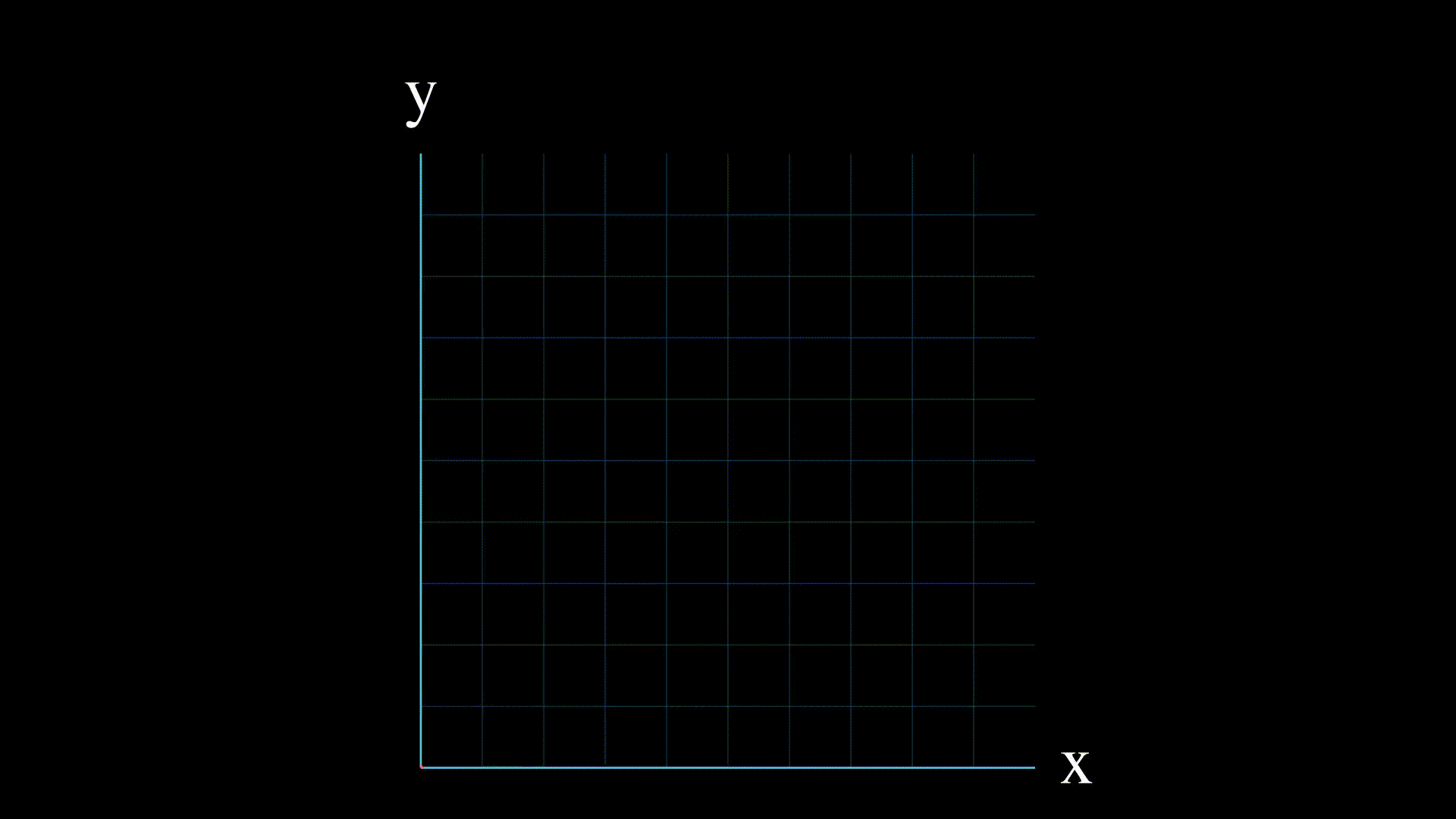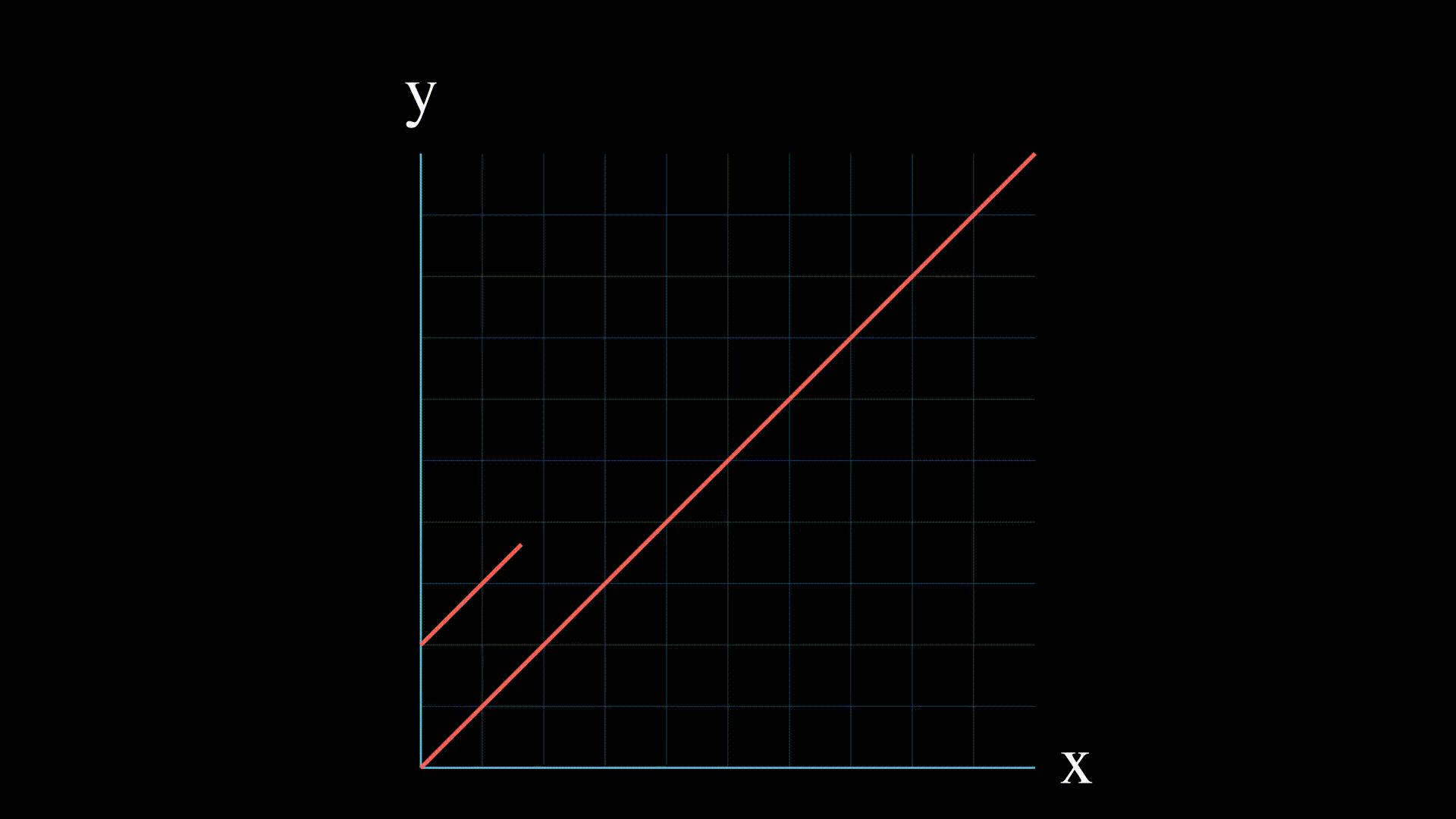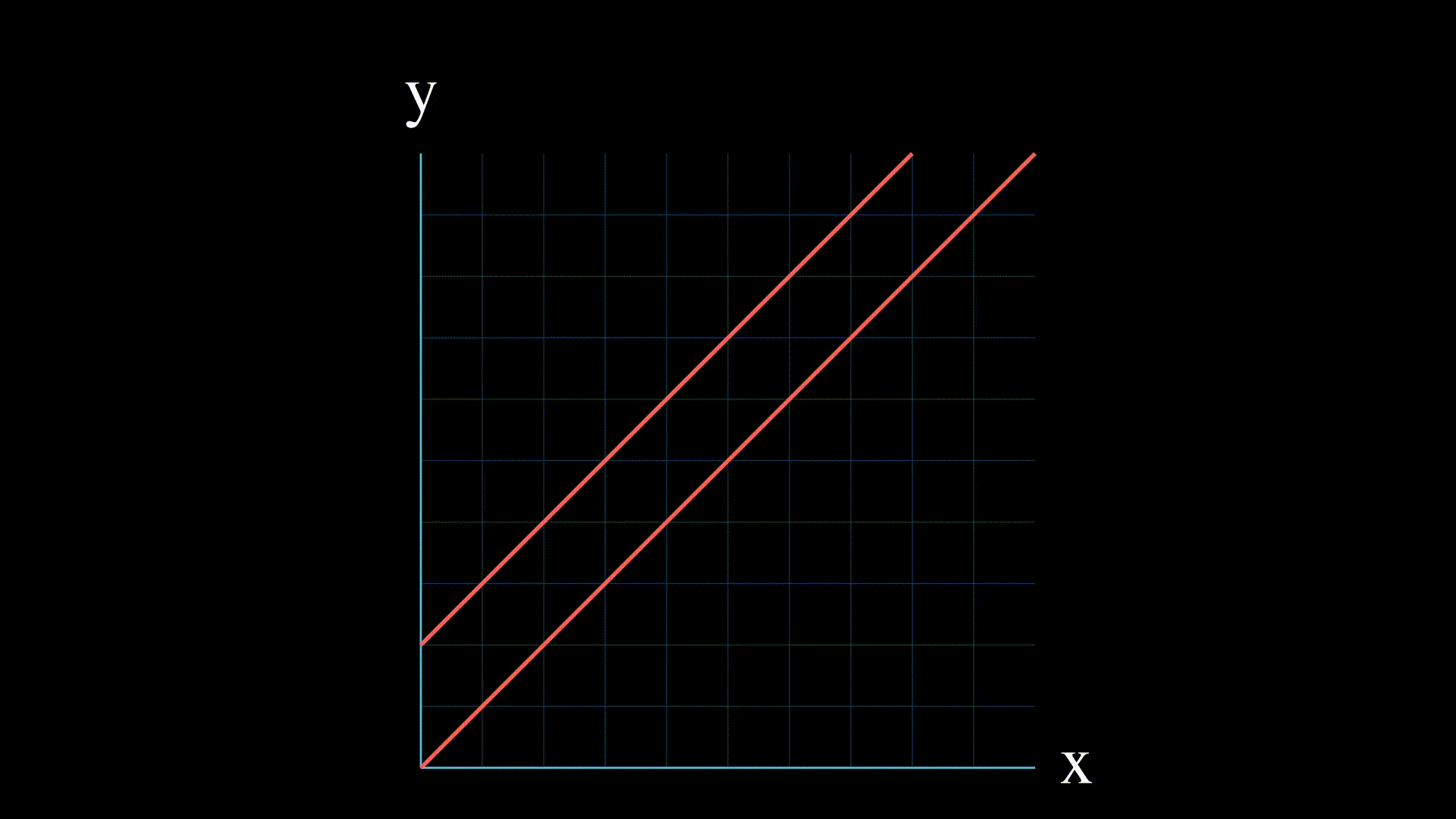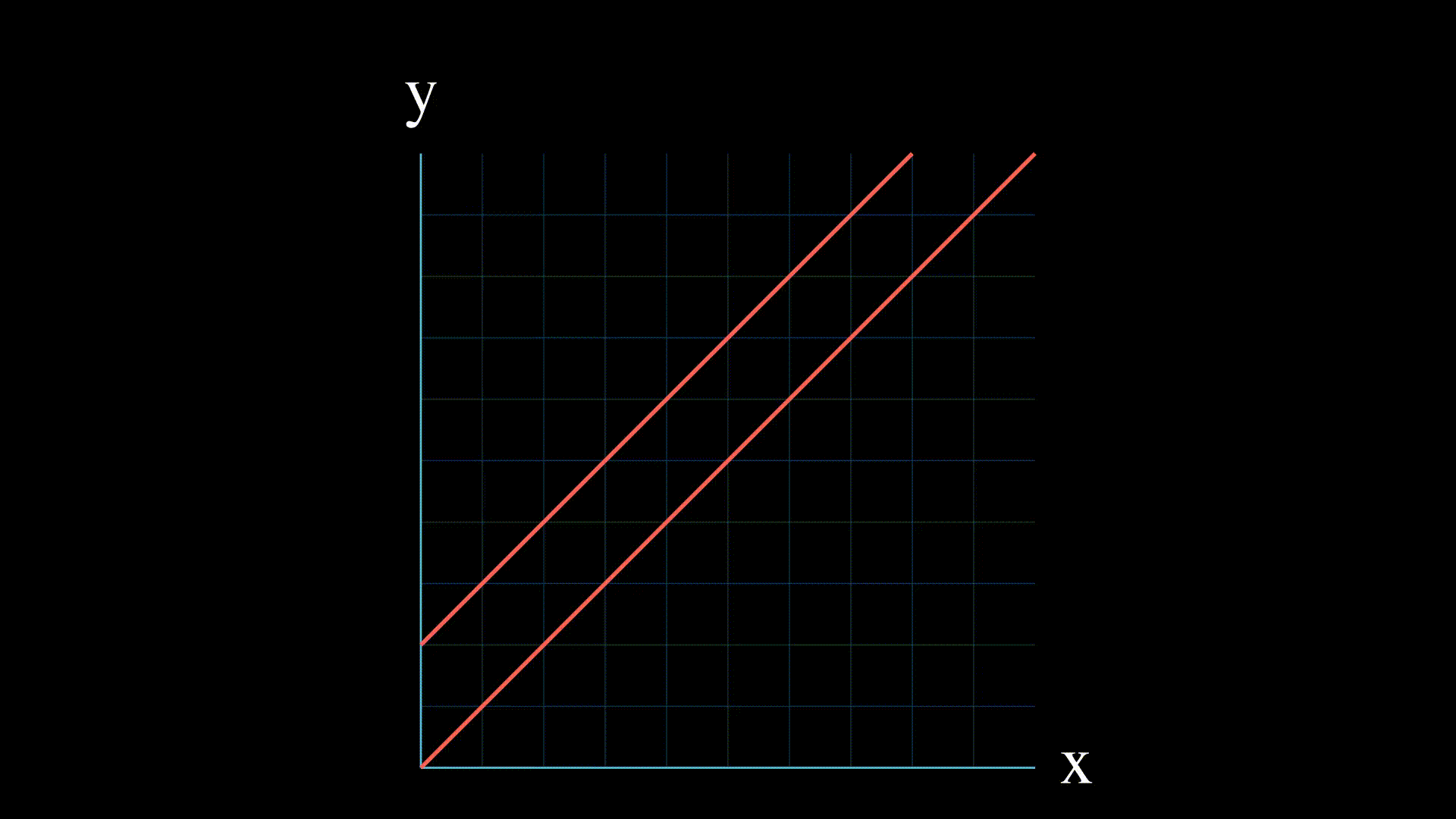
2. 一个解 这意味着直线在一个点相交。

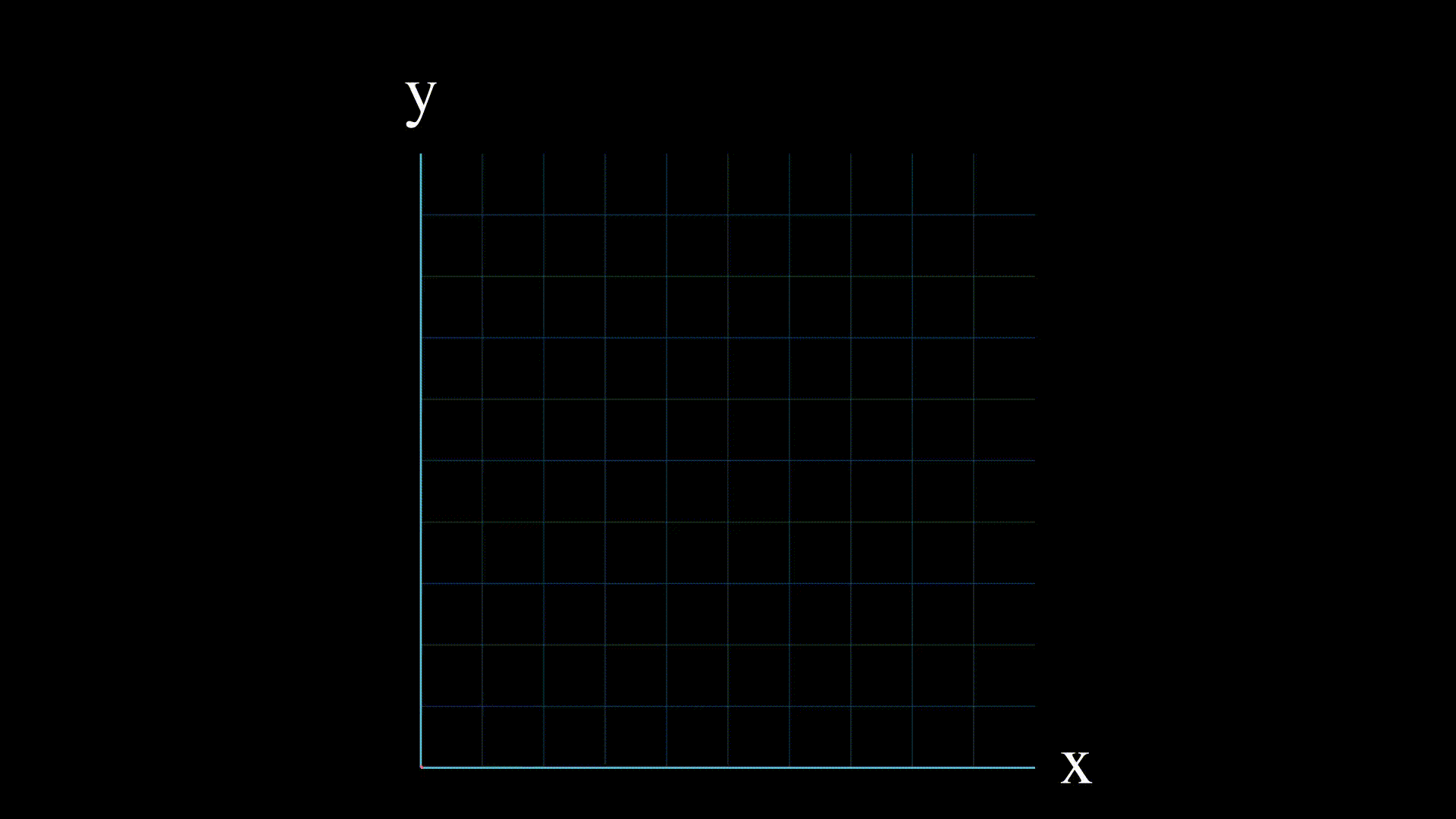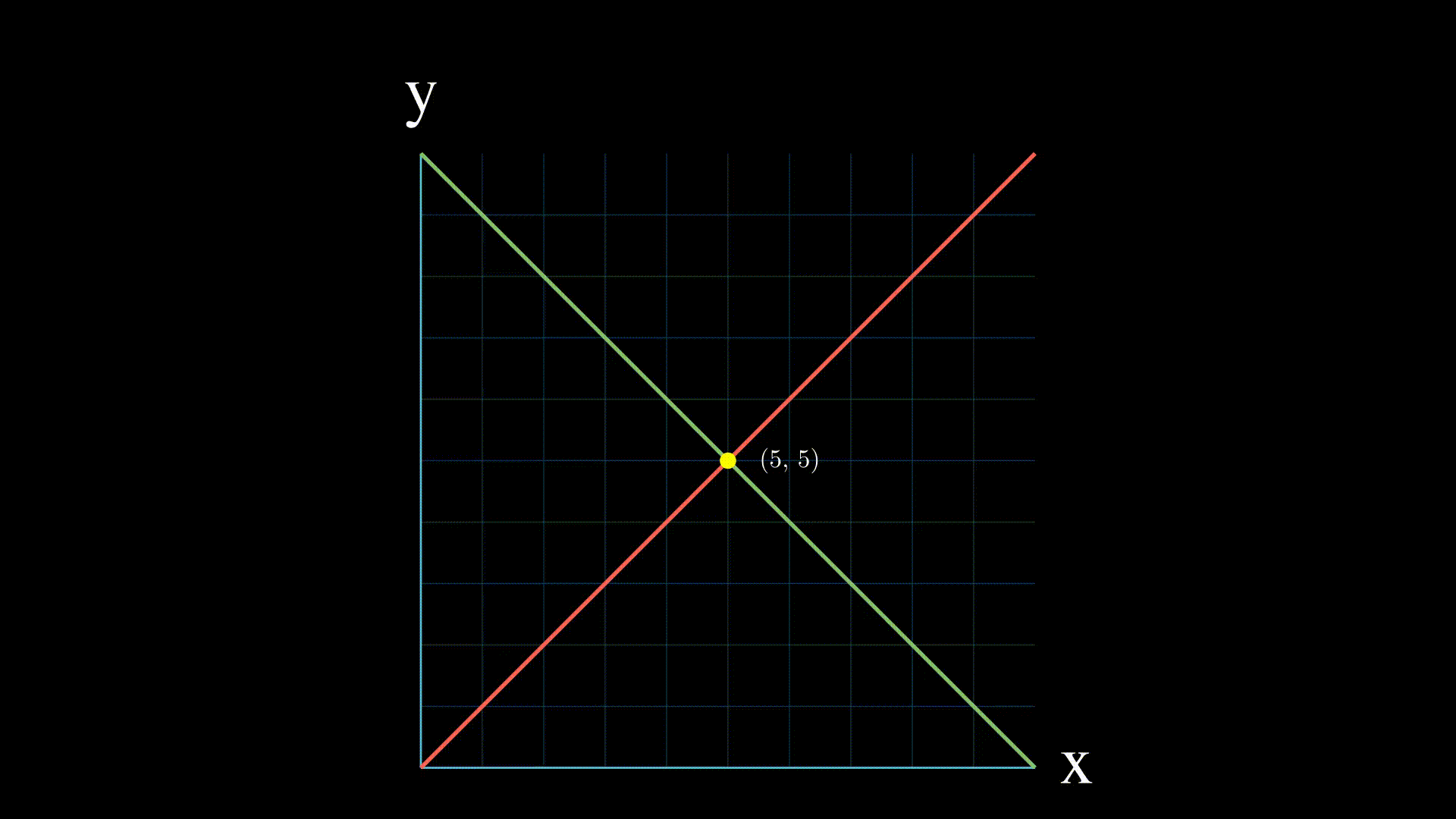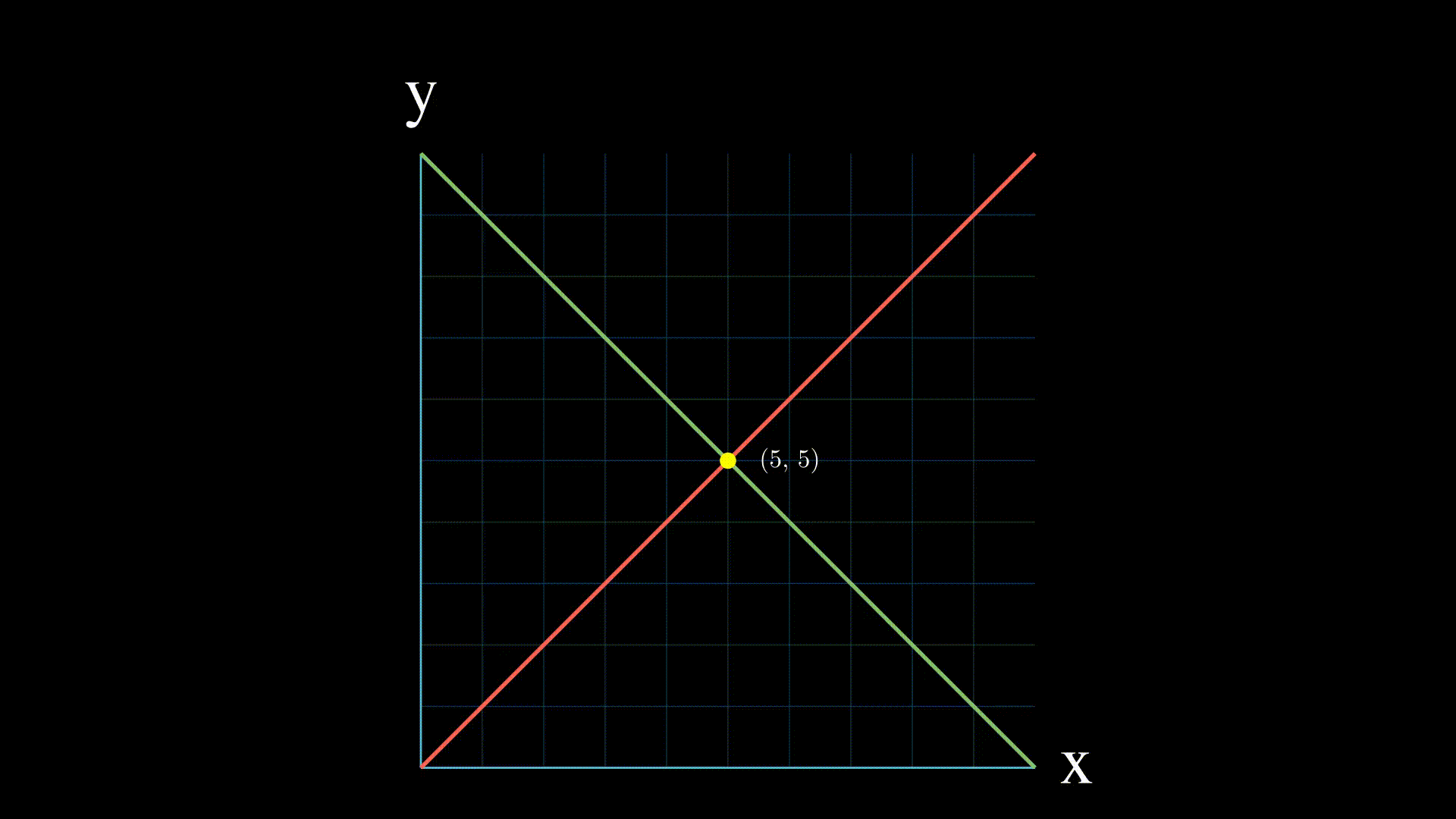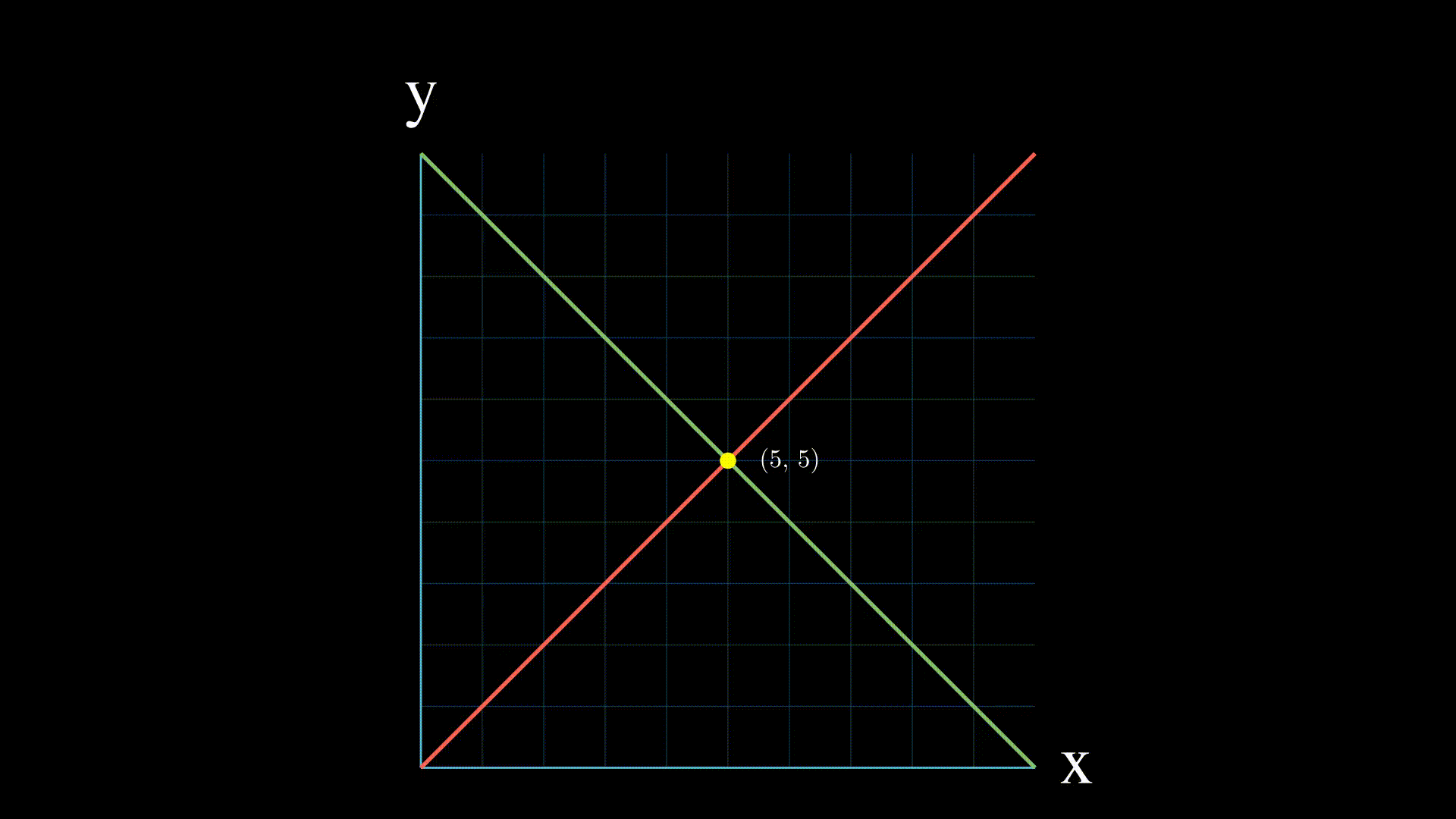
3. 无限解： 如果两个方程表示同一条直线，那么就有无限多的交点，线性方程组就有无限多的解。

有限域中的方程组同样具有：

1. 没有解或

2. 一个解或

3. $p$ 多个解，即与域的阶数同样多的解。

然而，仅仅因为某个实数的线性方程组具有零个、一个或无限个解，并不意味着相同的线性方程组在有限域中也会有零个、一个或 $p$ 个解。

我们强调这一点是因为我们使用算术电路和对信号进行赋值来编码在 NP 中求解我们的问题。然而，由于算术电路是用有限域编码的，可能会导致编码问题的方式不捕捉到我们试图建模的方程的行为。

以下三个示例显示了在有限域中方程组的行为如何发生变化。

示例 1：在常规数字中具有一个解的方程组在有限域中可能具有 $p$ 个解

例如，我们绘制：

$$x+2y=1$$ $$6x+y=6$$

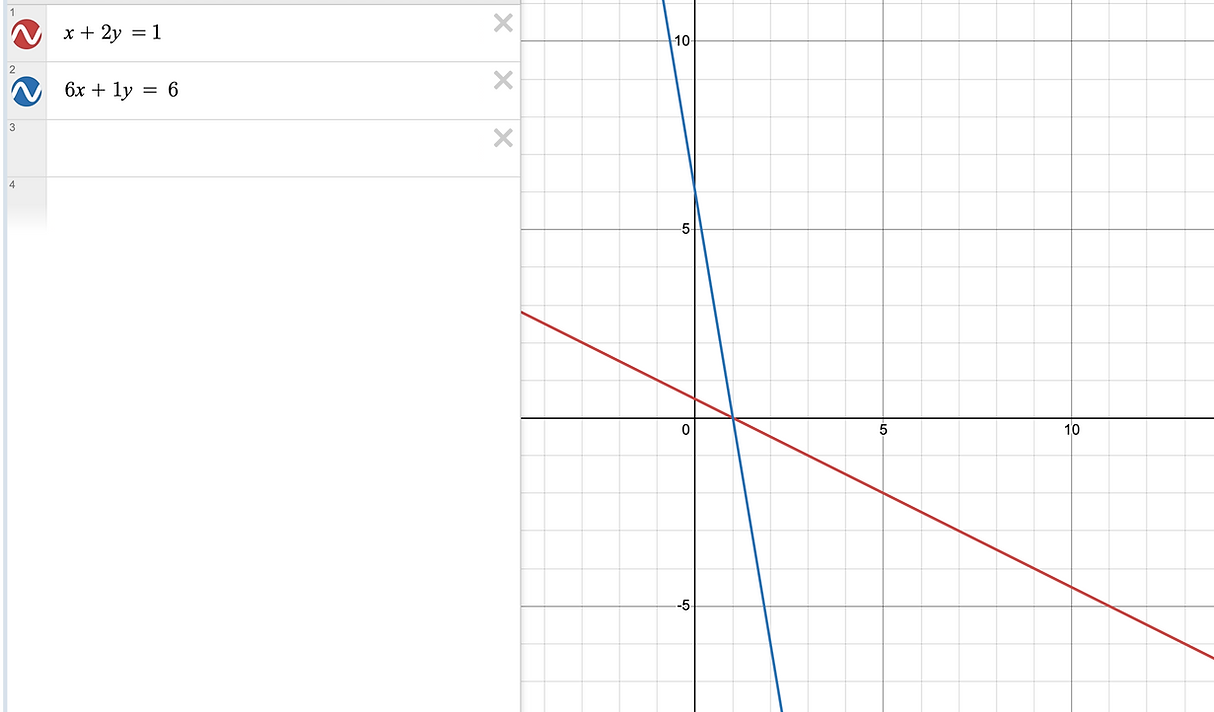
对于实数来说，解是 $(1, 0)$，但在有限域 $p = 11$ 中，它具有 11 个解：$\set{(0, 6), (1, 0), (2, 5), (3, 10), (4, 4), (5, 9), (6, 3), (7, 8), (8, 2), (9, 7), (10, 1)}$ 。

不要假设在实数中存在单一解的方程组在有限域中也存在单一解！

下面我们绘制有限域下的两个方程系统解，以说明两个方程的每个解都是相交的，实际上它们有相同的满足所有方程的点：

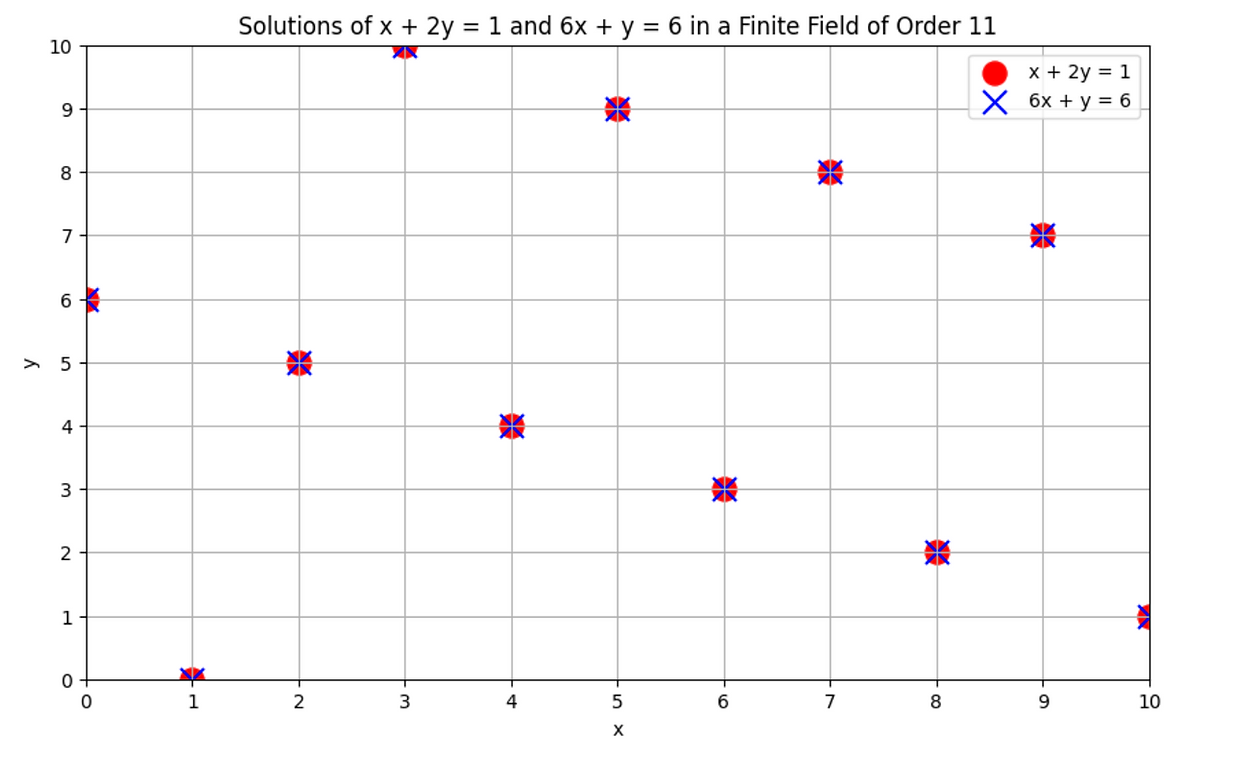
这可能看起来非常违背直觉——让我们调查一下它是如何发生的。若求解原方程：

$$x+2y=1$$ $$6x+y=6$$

得出 $y$：

$$y = 1/2 - 1/2*x$$ $$y=6-6x$$

$1/2$ 是 2 的乘法逆元。在模 $p = 11$ 的有限域中，6 是 2 的乘法逆元，即 $2 * 6 \pmod {11} = 1$。因此，$x + 2y = 1$ 和 $6x + y = 6$ 在有限域 $p = 11$ 中实际上是同一个方程。即方程 $y = 1/2 - 1/2x$ 在有限域中的编码是 $y = \mathsf{mul\_inv}(2) - \mathsf{mul\_inv}(2)x$ ，也就是 $y = 6 - 6x$ ，与该系统的另一个方程相同。

示例 2：在常规数字中具有一个解的方程组在有限域中可能没有解

同样出人意料的是，一个在实数中只有单一解的方程组，可能在有限域中没有解：

$$x + 2y=1$$ $$7x+3y=2$$

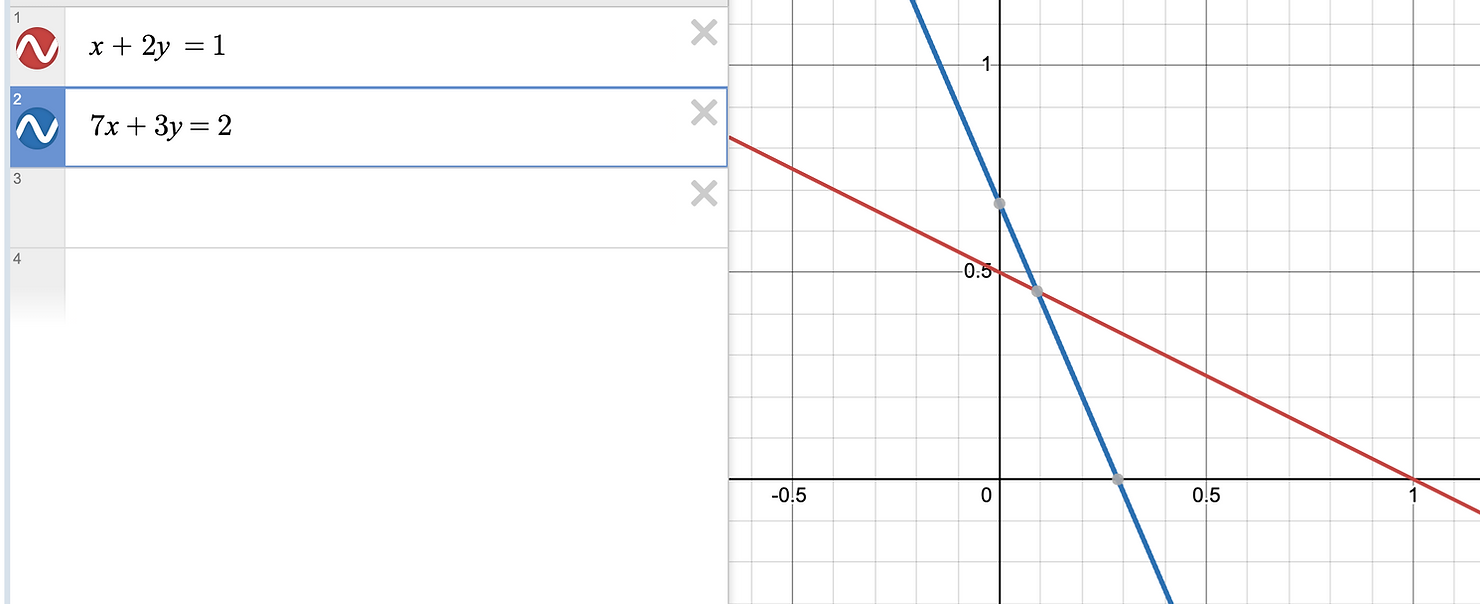
显然，该方程组有交点，但在有限域中没有解。

下面绘制有限域下的两个方程图：

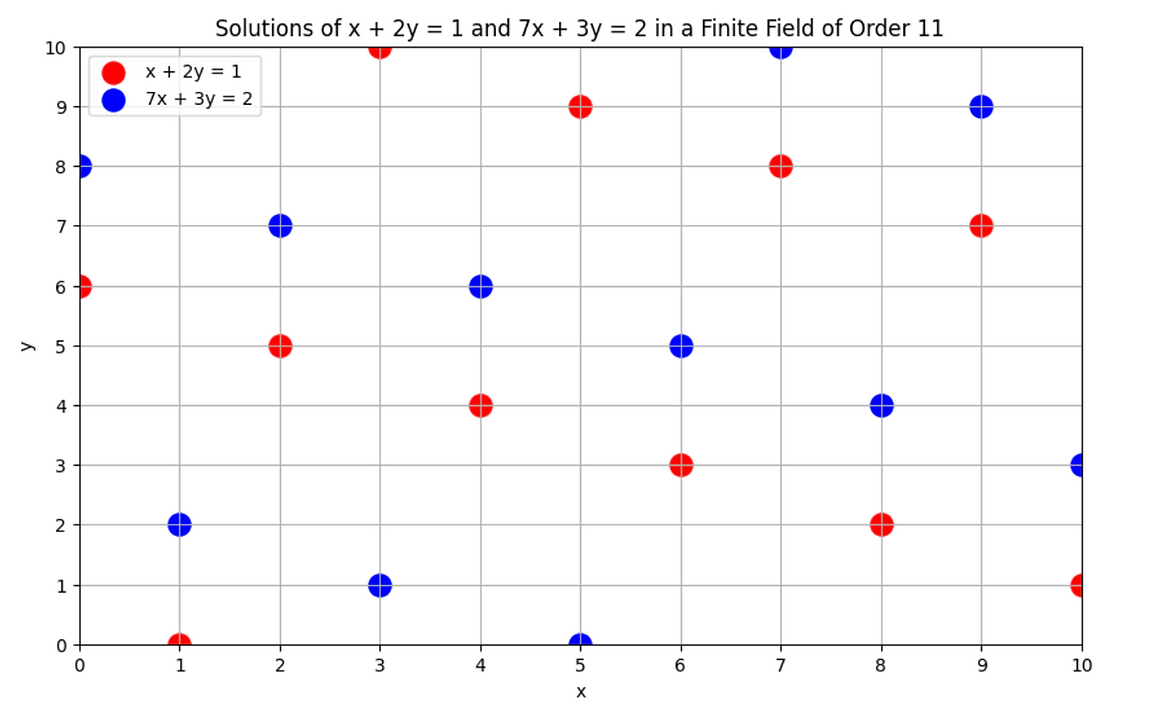
练习： 编写代码以暴力破解 (x, y) 的每种组合，范围为 x = 0..10, y = 0..10 ，以验证上述系统在有限域 $p = 11$ 中没有解。

为什么这个方程组在有限域 $p = 11$ 中没有解？

如果解如下：

$$x + 2y=1$$ $$7x+3y=2$$

将结果求解为实数，得到

$$ x = \frac{1}{11},\space y=\frac{5}{11} $$

上面的分数在有限域 p = 11 中没有同余元素。回顾一下，除以一个数字等同于乘以它的乘法逆元。同时，回忆一下，域的顺序（在这种情况下为11）不会有乘法逆元，因为域的顺序与0同余。

a 的乘法逆元是值 b，使得 a * b = 1。然而，如果 a = 0（或与之同余的任何值），则 b 没有解。因此，我们之前为实数写出的解不能转换为有限域的元素。

因此，上述解 (x, y) 不是有限域的一部分。因此，在有限域 p = 11 中，x + 2y = 1 和 7x + 3y = 2 是平行线。

从另一个角度看，我们可以求解方程以获得 y，并得到：

$$y = 1/2 – x/2$$ $$y=2/3-7x/3$$

我们在前一节中看到6是2的乘法逆元，所以第一个方程在有限域中的“斜率”是6。在第二个方程中，我们通过计算 7 乘以 3 的乘法逆元来计算斜率：(7 * pow(3, -1, 11)) % 11 = 6。我们现在展示它们在有限域中斜率是相同的。

斜率是 y = c + bx 形式中 x 的系数。对于上述两个方程，第一个斜率是 -1/2，而第二个斜率是 -7/3。如果我们将这两个分数转换为 p = 11 的有限域中的元素，我们得到相同的值5：

import galois
GF11 = galois.GF(11)

negative_1 = -GF11(1)
negative_7 = -GF11(7)

slope1 = GF11(negative_1) / GF11(2)
slope2 = GF11(negative_7) / GF11(3)

assert slope1 == slope2 # 5 == 5

这一事实对算术电路的影响是：

x + 2 * y === 1
7 * x + 3 * y === 2

算术电路在有限域 p = 11 中没有有效的赋值。

示例 3：在常规数字中有零解的方程组在有限域中可能有 p 个解

以下两个公式绘制的线是平行的，因此在实数中没有解：

$$x + 2y = 3$$ $$4x + 8y = 1$$

然而，在有限域 p = 11 中，它有11个解：$\set{(0, 7), (1, 1), (2, 6), (3, 0), (4, 5), (5, 10), (6, 4), (7, 9), (8, 3), (9, 8), (10, 2)}$。这些解绘制如下：

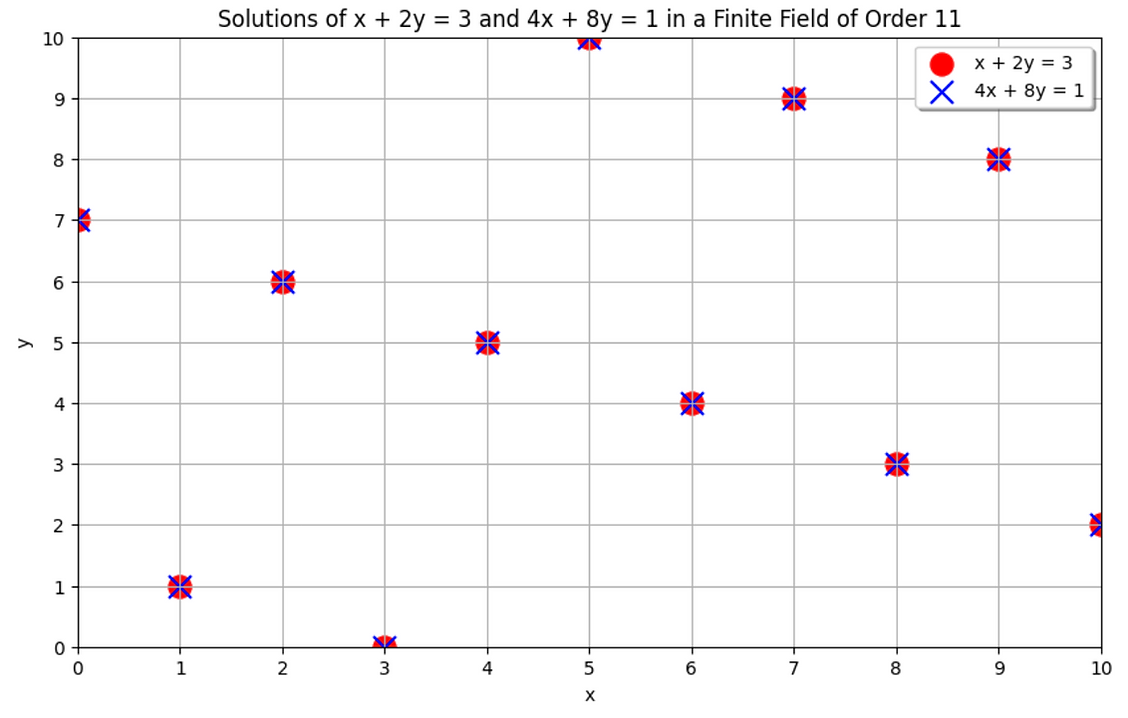
练习： 将两个方程转化为它们的有限域表示，看它们是否相同。

假设我们将这个方程系统编码为算术电路：

$$x + 2y = 3$$ $$4x + 8y = 1$$

x + 2 * y === 3
4 * x + 8 * y === 1

对于我们使用的有限域，即使它们“看起来不同”，我们的约束也是冗余的。也就是说，两个外观不同的约束实际上约束 $x$ 和 $y$ 具有相同的值。

有限域中的多项式

在算术电路一章中，我们使用多项式 x(x - 1) === 0 来强制 x 只能为0或1。这可以写成多项式方程。为此，我们完整扩展我们的表达式，直到它表示为单独的 $x$ 的幂，每个幂乘以一个系数。在这种情况下：x² - x === 0。

假设多项式 x² - x === 0 在有限域中（以及实数中）仅具有0或1的解是合理的。然而，在一般情况下，不应假设实数多项式的根在有限域中具有相同的根。我们将稍后展示一些反例。

尽管如此，有限域中的多项式与实数中的多项式共享许多性质：

• 一个度为 $d$ 的多项式最多有 $d$ 个根。多项式 $p(x)$ 的根是值 $r$，使得 $p(r) = 0$。
• 如果我们将两个多项式 $p_1$ 和 $p_2$ 相加，则 $p_1 + p_2$ 的度至多为 $\max(\deg(p_1), \deg(p_2))$。$p_1 + p_2$ 的度可能小于 $\max(\deg(p_1), \deg(p_2))$。例如，$p_1=x³ + 5x + 7$，而 $p_2 = -x³$，
• 在有限域中添加多项式遵循结合律、交换律和分配律。
• 如果我们将两个多项式 $p_1$ 和 $p_2$ 相乘，乘积的根将是 $p_1$ 和 $p_2$ 根的并集。

让我们绘制 $y = x² \pmod{17}$ 作为示例。

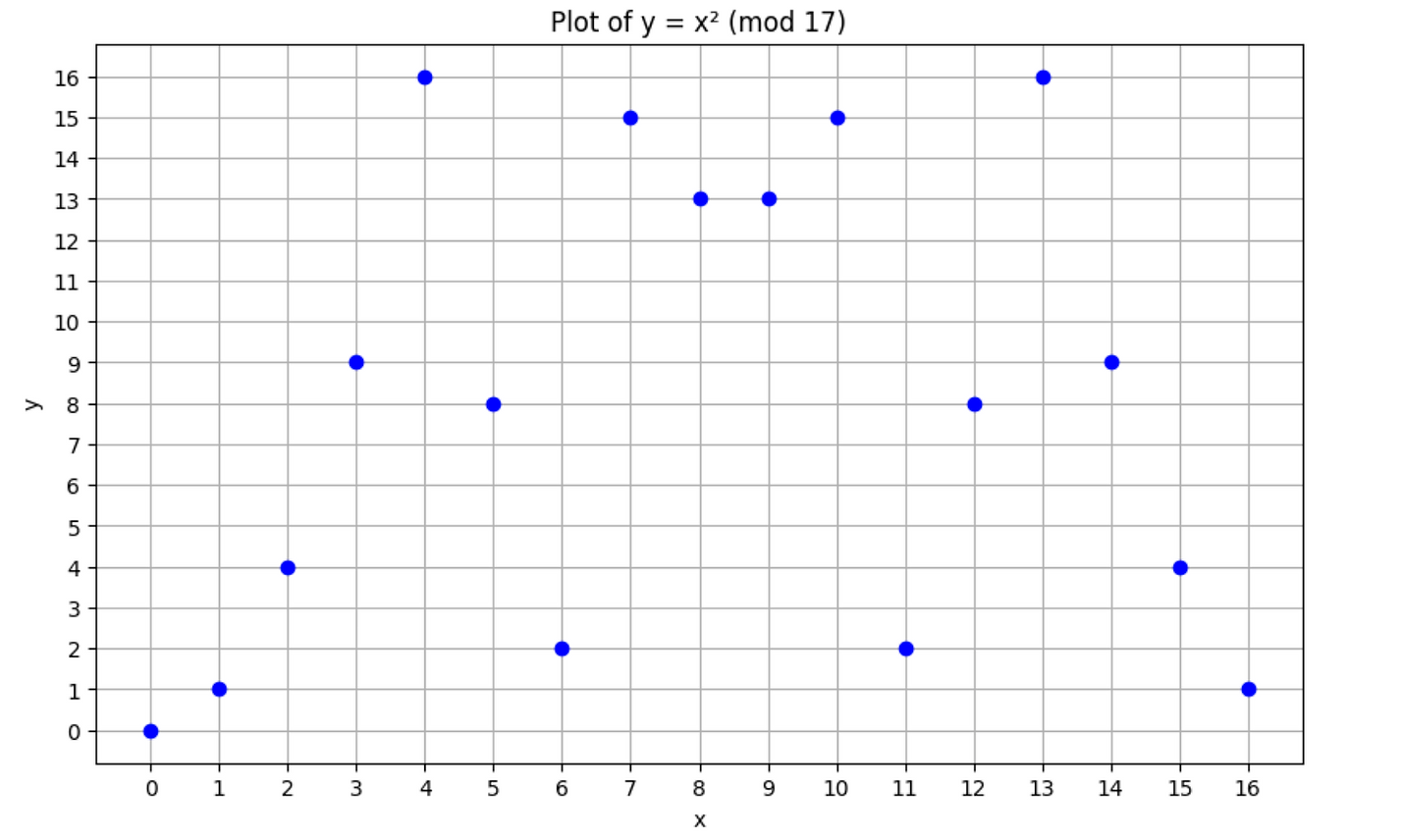
$x$ 的域是有限域的元素，输出（范围）也必须是有限域的成员。也就是说，请注意所有的 $x$ 和 $y$ 值都在区间 $[0,16]$ 内。有限域上的多项式只能具有小于 $p$ 的 $x$ 和 $y$ 值。

在有限域 p = 17 中，$y = -x²$ 的等价物是 $y = 16x² \pmod{17}$，因为16是该有限域中1的加法逆元。下图绘制了多项式 $y = 16x² \pmod{17}$：

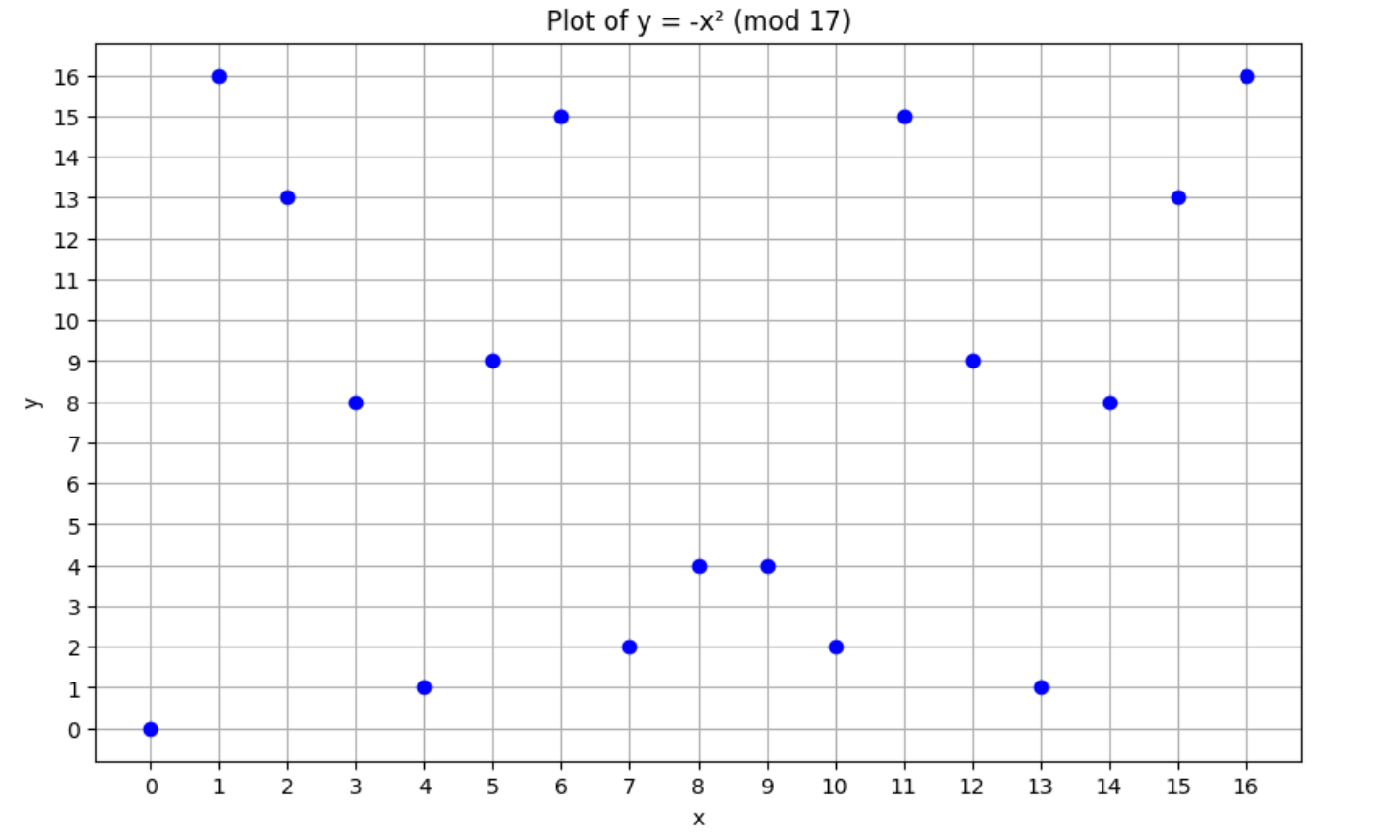
在实数中没有根的多项式在有限域中可能有根

正如我们之前谈到的线性方程组的例子一样，不应假设在实数中具有特定根的多项式在有限域中具有相同的根。

下面，我们在有限域 p = 17 中绘制 $y = x² + 1$。在实数中，$y = x² + 1$ 没有实根。但是在有限域中，它在 $4$ 和 $13$ 处具有两个根，红点如下：

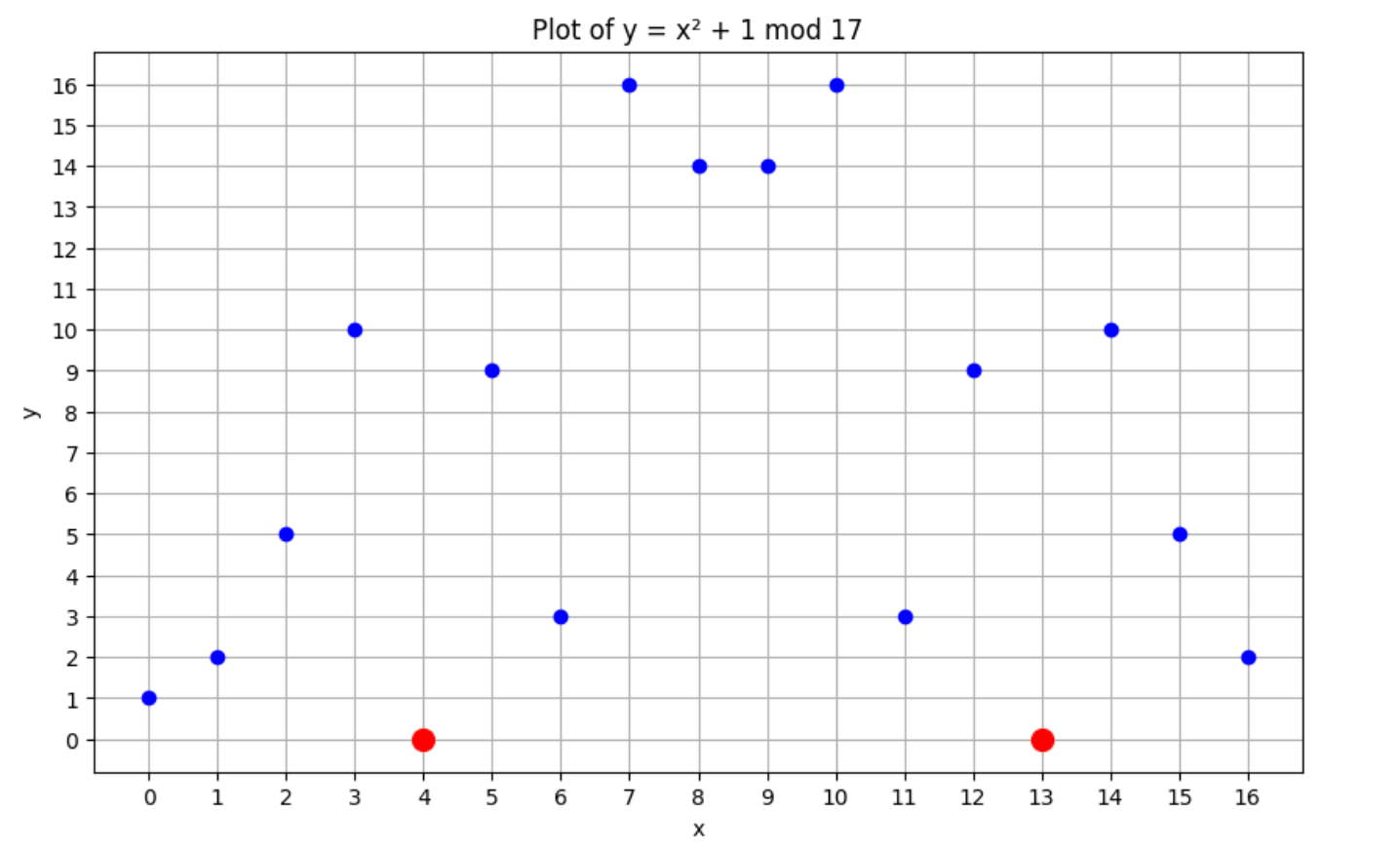
现在，让我们解释为什么 $y = x² + 1$ 在实数中没有根，但在有限域 p = 17 中有根。在有限域 p = 17 中，17与零同余。所以如果我们将一个值代入 $x$ 使得 $x² + 1$ 的值为17，则多项式将输出零，而不是17。我们可以求解 $x² + 1 = 17$ 得到 $x² = 17 - 1 = 16$。在有限域 p = 17 中，$x² = 16$ 的解是 $4$ 和 $13$。因此，$y = x² + 1$ 在有限域 p = 17 中的根是 $4$ 和 $13$。

在有限域中可能没有根的具有实根的多项式

考虑多项式 $y = x² - 5$。我们可以看到它的根是 $\sqrt{5}$ 和 $-\sqrt{5}$。然而，如果我们在有限域模17上绘制它，我们可以看到它永远不会穿过 x 轴：

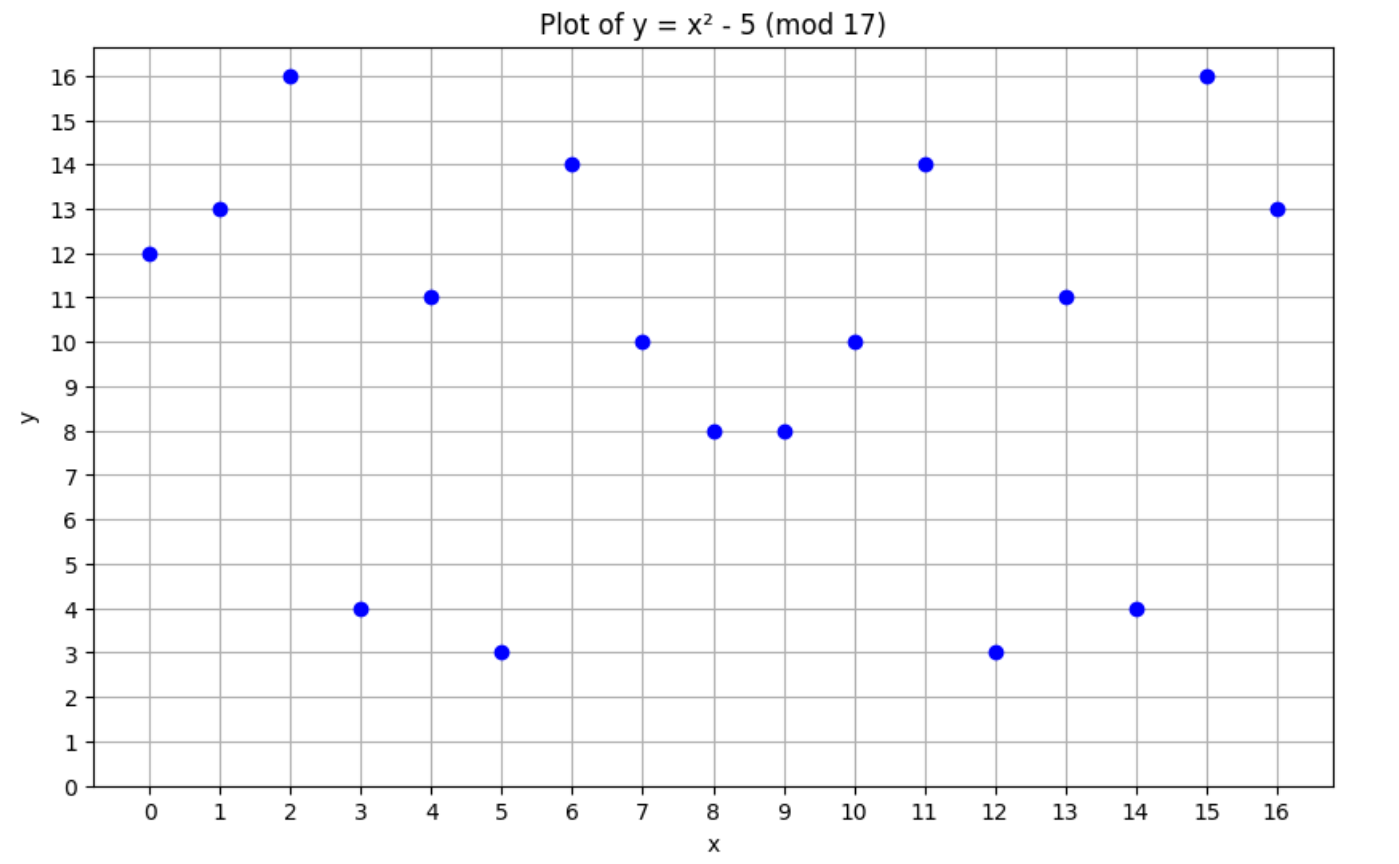
没有根的原因是 $\sqrt{5}$ 不能在模17的有限域中表示。然而，在有限域 p = 11 中，将会有两个根，因为5在有限域 p = 11 中有模平方根。

ZK 证明的算术电路中的局限性

如果我们希望编写一个算术电路来证明“我知道多项式 $y = x² - 5$ 的根”，而且是在有限域上执行的，那么我们可能会遇到无法编码 $\sqrt{5}$ 的问题。也就是说，在实数中，$y = x² - 5$ 具有根 $\sqrt{5}$，但这不能在某些有限域中表示。根据 $p$ 的不同，算术电路 x² === 5 可能没有有效的见证。

使用 Python 处理有限域中的多项式

在实验算术电路时，有时用 Python 代码进行模拟是有帮助的。当我们的算术电路具有多项式形式时，可以使用之前提到的 galois 库来测试其行为。以下代码示例展示了如何使用这个库来处理多项式。

在有限域中相加多项式

在下面的代码中，我们定义了两个多项式：p1 = x² + 2x + 102 和 p2 = x² + x + 1，然后将它们符号上相加，产生 2x² + 3x。请注意，在有限域 p = 103 中，常数项的系数相加为零。

import galois
GF103 = galois.GF(103) # p = 103

## 我们定义一个多项式 x^2 + 2x + 102 mod 103
p1 = galois.Poly([1,2,102], GF103)

print(p1)
## x^2 + 2x + 102

## 我们定义一个多项式 x^2 + x + 1 mod 103
p2 = galois.Poly([1,1,1], GF103)

print(p1 + p2)
## 2x^2 + 3x

galois 库足够智能，可以将负整数解释为加法逆元，如下面的代码所演示：

import galois
GF103 = galois.GF(103) # p = 103

## 我们可以输入 "-1" 作为系数，它将
## 自动计算为 `p - 1`
## -1 在模 103 的域中变为 102
p3 = galois.Poly([-1, 1], GF103)
p4 = galois.Poly([-1, 2], GF103)

print(p3)
## 102x + 1
print(p4)
## 102x + 2

在有限域中相乘多项式

我们可以将多项式相乘：

print(p3 * p4)
## x^2 + 100x + 2

请注意，p3 和 p4 是度1的多项式，而它们的乘积是度2的多项式。

在有限域中查找多项式的根

在有限域上查找多项式的根是一个单独的话题（请参见维基百科有关 在有限域上因式分解多项式 的页面）。galois 库可以使用 roots 函数执行根的计算。这可能对验证多项式形式的算术约束实际上创建了预期的约束很有用。

print((p3 * p4).roots())
## [1, 2]

galois 库的限制

该库会安静地对作为系数传递的浮点数取整：

## galois 库会安静地将
## 浮点数转换为整数
galois.Poly([2.5], GF103)
## Poly(2, GF(103))

如果传入大于或等于 p 的数字，库将还原：

## 下面的代码失败，因为我们不能
## 有系数等于域阶或更高的数字
galois.Poly([103], GF103)
## ValueError: GF(103) arrays must have elements in `0 <= x < 103`, not [103].

通过 RareSkills 了解更多

请参见我们的 ZK Book 了解有关零知识证明的更多信息。

练习题

在下面的问题中，使用有限域 p 为 21888242871839275222246405745257275088548364400416034343698204186575808495617。请注意，galois 库初始化这样大小的 GF 对象 galois.GF(p) 需要一些时间。

1. 一名开发人员创建了一个算术电路 x * y * z === 0 和 x + y + z === 0，打算约束所有信号为零。找到一个反例，使约束得到满足，但不是所有的 x、y 和 z 都为零。
2. 一名开发人员创建一个带有多项式 x² + 2x + 3 === 11 的电路，并证明2是一个解。另一个解是什么？提示：将电路写成 x² + 2x - 8 === 0，然后手动因式分解该多项式以找到根。最后，计算根在有限域中的同余元素，找到另一个解。

最初于 2024年4月29日发布

• 原文链接： rareskills.io/post/finit...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～