密码学101：承诺方案再探

这是关于密码学的一系列文章中的一部分。如果这是你遇到的第一篇文章，我强烈建议你从系列的开头开始。

好的！到目前为止，我们已经在_基于身份的密码学_的背景下看到了配对的应用。但我们也看到，配对本身是强大的，可以实现不依赖于 身份 的其他方法。在这篇文章中，我希望能针对这个想法进行扩展。

现在是时候重新审视几篇文章前提到的一个概念：承诺方案 。我们之前定义了它们：以不提前透露的方式承诺某个 值。

这算是一种密码学反作弊机制。

这次，我们将看一个还没有提到的承诺方案类型：多项式承诺 。具体来说，要呈现的方法是这篇论文中描述的：KZG（Kate-Zaverucha-Goldberg）承诺。

简短的免责声明

我相信，到目前为止，在这个系列中，给文章贴上 101 的标签将会比较困难——因为它们不再 那么 入门。尽管如此，这些展示的精神是为了让论文中相对晦涩的内容和符号变得更容易接触。从这个意义上说，确实是我去掉了一些复杂的元素——即便如此，这并不意味着这些主题会变得更容易。

尽管如此，如果你已经阅读到这一点，可能意味着你非常致力于理解复杂的密码学概念。所以，恭喜你为此付出的努力，感谢你的阅读，我希望你仍然觉得内容有用！

提交给多项式

到目前为止，我们对承诺方案的描述只涵盖了一个场景，那就是有一个我们不想提前透露的秘密值。而_打开_承诺的意思就是_揭示_这个值。

但如果我们能拥有一个完整的 承诺工厂 呢？

也就是说，如果我们能够承诺一个 函数 ？那么我们所能做的就是向验证者提供函数的 评估值 ，而他们可以使用我们的承诺来检查其 正确性 。

什么？

公平地说，尽管这听起来像是一个很有趣的想法，但不 Immediate clear 是否有任何合适的应用。

为了保持你们的积极性，我想说：对一个函数进行承诺是我们将在将来的文章中要关注的一些_零知识证明_的关键成分。

此外，回想一下，当我们谈论门限密码学时，我们提到过某些情况需要可验证的秘密共享。即，不仅需要某个多项式的评估值，而且还需要其正确性的证明。

多项式承诺方案可以对此提供帮助。

背景是（有点儿）设定好了。也许一个图解会帮助澄清我之前的意思：

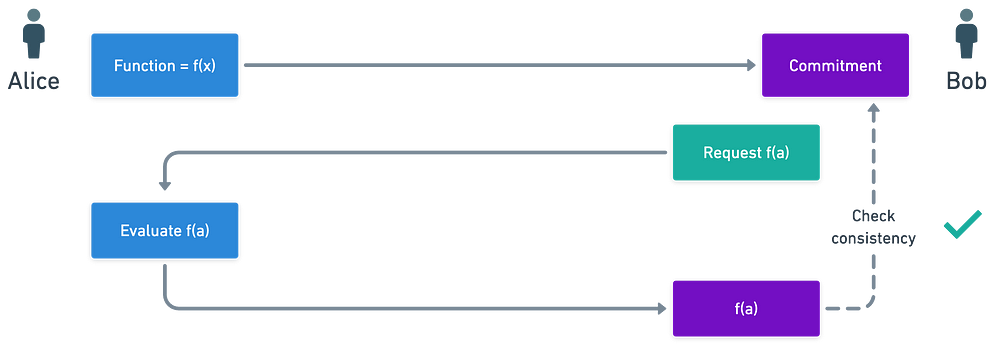
大体来说，我们计划要做的事情

注意，在上面的图示中，函数 f 是 秘密的 ，并且从未真正披露。正如你现在可能猜到的那样，_一致性检查_将借助于_配对_进行。

话虽如此，让我们直接进入正题。

设置

我们的承诺方案将由至少_三个步骤_组成。论文本身描述了大约六个算法，但我们可以简化一些，以使解释更易懂。

首先，我们需要_两个_次序为_n_的群体：我们称它们为𝔾₁和𝔾₃。我们还需要一个𝔾₁的生成元，我们将其表示为G。这些群体的生成方式是存在一个对称配对（或[自配对](https://medium.com/@francomangone18/cryptography-101-pairings-e50520deea6c#:~:text=If%20you%20check,to%20be%20disjoint.）形式如下：

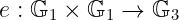
而这将是我们拼图中至关重要的一部分。

此外，由于我们将处理多项式，这次我们将更喜欢_乘法记号_来表示𝔾₁中的元素；也就是说，该组将有如下形式：

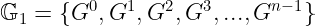
重要说明：由于G将是多项式的输入，我们通常以椭圆曲线群来展示实例，因此我们面临一个问题：椭圆曲线上的点是通过标量乘法（即[s]G）相乘，而不是进行指数运算。

为了缓解这个问题，我们可以利用同构关系转换为乘法群，使用类似的推理，如这里解释的.

所以实际上，Gˢ将仅意味着[s]G。

很好，很好。有了这些，我们可以真正开始设置系列的...