密码学 101：零知识证明（第 2 部分）

这是一系列关于密码学的文章中的一篇。如果这是你第一次阅读本系列文章，我强烈建议你从本系列的开篇开始。

在过去的几篇文章中，我们涵盖了许多基础构件。现在终于到了将这些乐高积木组合成一个协议的时候了。万岁！

请记住，我们之所以如此努力理解这些动态部分，是为了尝试为零知识证明构建一个通用框架——因为正如我们所看到的，为特定应用创建协议有些不切实际，需要专门的研究。

现在，我们准备引入一个利用我们预先定义的每个元素的知识证明家族：SNARKs。

具体来说，我们将研究一个名为Plonk的方案。要全面了解该技术，请参考此处。我会尽力尽可能准确地解释它。此外，这并不是唯一符合SNARK标准的协议。还存在其他机制，如Groth16、Marlin和Halo。我可能会在未来探讨这些内容，但现在，我只在这里留下几个链接，以防你想满足好奇心！

免责声明

这篇文章会很长，而且说实话，很复杂。也就是说，可能比平常更难。对于一个非常复杂的协议，我能简化解释的余地实在有限。

但是，如果要用一句话概括整个过程，那就是：

在 Plonk 中，我们将电路的计算编码为一系列多项式，这些多项式代表电路施加的约束，通过一系列测试来证明陈述，而无需揭示多项式本身——从而不泄露秘密输入。

要完全理解这将是一次疯狂的旅程。我们需要涵盖几个要素。以下是计划的概述，也可作为目录：

提示：你可以通过 command + 点击跳转到链接部分！

• 电路作为约束集合
• 将电路编码为多项式.-,Encoding%20the%20Circuit,-Having%20said%20all)
• 列出验证要求
• 验证技术
• 验证

此外，我假设你已经阅读了关于多项式承诺方案的文章，以及关于算术电路的文章。如果还没有，我强烈建议先阅读它们！

闲话少说，我们开始吧！

什么是 SNARK？

这个缩写代表简洁非交互式知识论证（Succinct Non-interactive ARguments of Knowledge）。用简单英语来说：一种证明知识的机制，具有简洁（或短小）和非交互的特点。我们需要在此剖析几点，以更好地理解构造的目标：

• 简洁意味着我们生成的任何证明在大小上必须小，且验证时间快。
• 非交互意味着验证者在收到证明后，无需与证明者进一步交互。稍后会详细说明。
• 最后，我们说这是一种知识证明，但不一定是零知识证明（尽管它可以是）。特别是，Plonk由于其构造方式，符合零知识标准。

别担心——我们暂时还不能构建SNARK。我们需要先涵盖几个概念。

重温电路

在之前的文章中，我们看到了算术电路如何优雅地表示计算，以及如何为陈述的验证制定方案。

因此，证明者的目标将是试图说服验证者，他们知道某个秘密值 x——实际上是一个值的向量——满足：

证明者不想揭示x，同时，我们也不希望验证者运行昂贵的电路计算。因此，实际发生的情况是，证明者将评估电路，然后将输入和每个门的结果（也称为计算轨迹）编码。

以下是一个使用域 𝔽₁₁₃ 的评估示例：

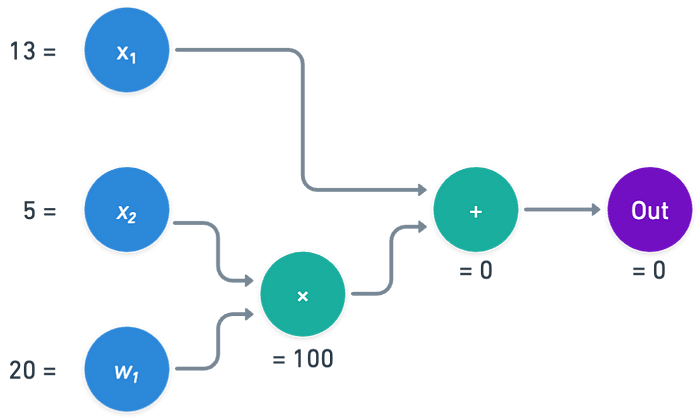
注意：在本例中，我们使用模 n = 113

我们可以将此评估视为以下轨迹，以表格形式可视化：

+-----------+------+------+------+
|           |  w1  |  x1  |  x2  |
+-----------+--------------------+
| inputs    |  20  |  13  |  5   |
+-----------+--------------------+

+-----------+--------------+---------------+----------+
|           |  left input  |  right input  |  output  |
+-----------+--------------+---------------+----------+
| gate 0    |  5           |  20           |  100     |
+-----------+--------------+---------------+----------+
| gate 1    |  13          |  100          |  0       |
+-----------+--------------+---------------+----------+

包括Plonk在内的现代 SNARK 的绝妙思想是将此轨迹编码为多项式，最终使验证者能够检查计算的有效性。这里的有效意味着遵循一组特定的约束。即：

• 每个门被正确评估
• 线（具有相同来源）具有相同的值

这里的线指的是电路中门之间的连接或输入到门的连接。我们可以将这些线视为保存电路的值，而不是节点本身：

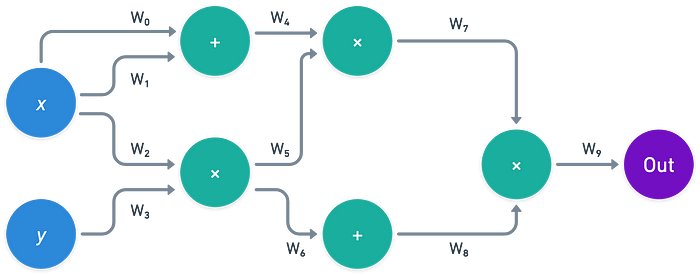
在此图中，你可以看到某些线应保持相同的值：W₀、W₁和W₂，以及W₄和W₅。此外，门应有意义——例如，W₀ + W₁应等于W₄。

电路既可以作为计算的方案，也可以作为要检查的约束集合！

每组约束——线值、门约束和布线约束——将被编码到不同的多项式中。

例如，整个计算轨迹可以编码为单个多项式P，其中P(xᵢ)对应于某条线。

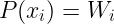
我们有线值Wᵢ，但需要选择将哪些xᵢ值编码到其中。使用某些整数是完全可以的选项——比如集合{0,1,2,3…,N}。但使用域 𝔽ₚ 的单位根会带来更多好处。

嗯？

单位根

我之前提到过这个概念，但像《黑客帝国》中的尼奥一样避而不谈。现在正是深入理解即将出现的符号的好时机。

因此，定义如下：如果满足以下条件，我们称值ω（希腊字母 omega）为域 𝔽ₚ 的k 次单位根：

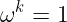
在这种情况下，集合H：

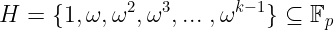
同时也是一个由ω生成的循环乘法群：

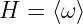
使用此集合中的元素作为编码多项式P(X)的输入有两个好处。首先，从一个单位根移动到下一个单位根，只需乘以 ω。同样，向后移动则是乘以ω 的逆元。并且它是循环的：根据定义：

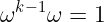
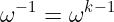
其次——也是最重要的部分——使用此集合允许我们使用最高效的算法进行插值：快速傅里叶变换。我们不会深入探讨其工作原理（至少现在不会！），但要知道这大大缩短了插值时间——这意味着生成证明的速度更快（相较于其他插值方法）。

编码电路

说了这么多，是时候进入正题了。实际看看计算轨迹是如何被编码的。

我们用|I|表示电路的输入数量，用|C|表示门的数量。由此，我们定义：

![](https://img.learnblockchain.cn/2025/02/18/1VEY7wMSen3ebUA6g6HRxjA...