密码学基础：环（Ring）上学习错误问题

这是关于密码学的一系列文章中的一部分。如果这是你第一次接触这系列文章，我强烈建议你从 系列的开头 开始。

在我们之前的文章中，我们介绍了另一个供我们研究的结构：环。这些将为一些根本上不同于我们迄今所见的密码学打开一些新的道路。

不过，让我们不要急于求成——在尝试理解任何新的加密技术之前，还有一件事需要做。

没有任何方法在实践中是可用的，除非它是安全的。在此系列的这个阶段，我们完全清楚安全性是通过破解一个方案的难度来衡量的。

例如，解密一条加密消息而不知晓私钥有多难？

为了回答这个问题，我们需要理解假定为困难的相关数学问题。在这个系列中，我们已经见到了一些这样的例子——比如说整数因子分解问题和离散对数问题。

当然，还有更多这样的问题。今天，我们将学习一个全新的问题，它将成为基于环的密码学的基础。

好了，让我们看看我们正在处理什么！

设置准备

环学习错误（Ring Learning With Errors，简称 RLWE）是一个基于多项式的问题。准确地说是一个商多项式环。简要回顾一下，这意味着我们将与某个环一起工作：

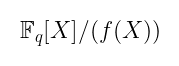
这样我们就可以将任何多项式对f(X)进行模约——即模多项式。

我们在 前一篇文章 中详细解释了这一点，所以如果需要，可以去看看！

那么……我们可以对此做什么？

让我们逐步开发我们的理解。给定几个多项式A(X)和S(X)，我们可以计算它们的乘积，如下所示：

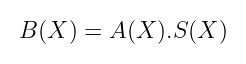
在这一点上，环的属性发挥作用：B(X)根据选择的某个多项式f(X)进行模约，确保次数始终是有界的。

这里有一个问题：如果我给你B(X)和A(X)，你认为恢复S(X)的难度有多大？

嗯，这并不难！

事实证明，根据仔细选择的f(X)，环中的每个多项式都可以反转。它的工作原理与有限域中的模逆完全一样：对于每个多项式P(X)，我们可以找到某个P⁻¹(X)，使得：

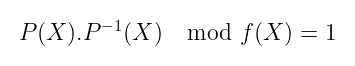
拥有这个工具使得任务变得相当简单：你只需找到A⁻¹(X)并计算：

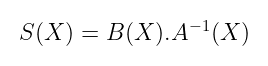
好的，这似乎不是一个良好的困难问题的候选者。或者说是？那我们来稍作修改？

转变方向

只需稍微调整一下，我们就可以将这个看似无害且易于解决的表达式转变为更有用的东西。这真的很简单——我们需要做的就是将一些错误或噪声多项式混入其中：

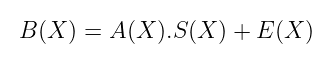
这个错误需要是小的——只要有一点噪声就足够了，正如下文所说的万事皆是如此_。

就这样！这一转折相当特别，因为我们已经习惯了疯狂的事情。

这个看似微不足道的调整隐藏了很多复杂性。让我们稍作思考。

稍微重新组织一下这个表达式：

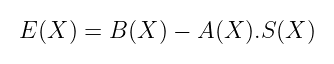
从这个角度看，很容易看出，给定任何多项式A(X)和B(X)，我们基本上可以选择任何S(X)并计算E(X)。这意味着没有唯一或直接的方法将A(X)与B(X)联系起来。解决方案不再是直接的。

听起来很有希望！

但在我们继续进行一个例子之前，还有一些事情需要谈谈。“学习与错误”中的学习是什么？

学习问题

在这一部分，我们需要再次改变视角。别担心——没有什么奇怪的。这次一切都会很友好。

我不再信任你了。

与其直接使用多项式A(X)和B(X)，不如先来看看它们的评估。所以，我们将为X选择一些值并计算：

这些向量显然是相关的——它们遵循我们之前描述的多项式方程：

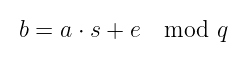
顺便提一下，依次乘以a⋅s就是分量乘法。

如往常一样，问题是， 这有什么用 ？随着我们探讨一些应用，这个答案会变得更清晰！耐心点。

现在的问题是：

给定a和b，找到s。

沿着先前讨论的思路，只要e被仔细选择——意味着它是从特定分布中随机抽取的，那么这个问题就非常困难。想象一下类似于正态分布。

之所以难，是因...