密码学基础：协议大全

这是关于加密技术的系列文章的一部分。如果这是你遇到的第一篇文章，我强烈建议从系列的开头开始阅读。

好的！我们已经走了很远。我们已经掌握了群（groups）（特别是椭圆曲线）和哈希作为我们可用的工具，并且我们已经看到了它们的实际应用。

但是，我们知道的东西可以做更多的事情。本文将致力于列出和解释基于椭圆曲线的加密协议。

我必须指出，相同的协议可以使用模 q 的整数群构造。我们将坚持使用椭圆曲线，因为这样做有一些好处。这种讨论会在另一个时间进行。

这个列表绝不是 完整的 — 还有更多的内容。不过，这应该能为你提供一个良好的基础，让你很好地理解到目前为止我们所知道的可能性。

系好安全带，让我们直接进入主题吧！

密钥交换

还记得对称加密的例子吗？它依赖于使用一个共享密钥。我们简要提到，在不安全的信道上共享密钥并不是一个好主意 — _任何人_都可能在窃听。如果他们在窃听，并且掌握了共享密钥，那么他们可以解密任何后续的消息！

幸运的是，有一些机制可以安全地生成共享密钥。最常见的技术是Diffie-Hellman 密钥交换算法。这个方法最初是使用模 q 的整数公式制定的，但可以轻松扩展到椭圆曲线 — 我们得到的就是所谓的椭圆曲线Diffie-Hellman （ECDH）方法。这是它的样子：

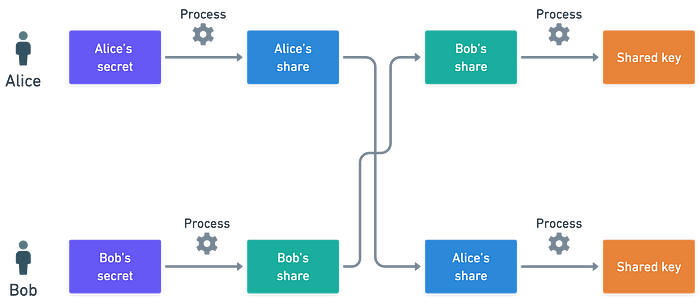
这个想法很简单：Alice 和 Bob 想要_结合_他们各自的秘密，以生成一个共享密钥。

创建共享密钥

为此，Alice 和 Bob 先就要使用的椭圆曲线和该曲线的一些生成元_G_达成一致。假设Alice选择一个秘密整数a，而Bob选择另一个秘密整数b。他们如何结合这些秘密？

• Alice 计算A = [a]G，然后将其发送给 Bob。请记住，Bob 不可能从_A_恢复a — 这非常困难。
• Bob 接收A，并计算S = [b]A = [b]([a]G) = [b.a]G。

Bob 还发送B = [b]G，而 Alice 也计算S = [a]B = [a]([b]G) = [b.a]G。看到了吗——他们都计算出了相同的点S！

这点有趣的地方在于，任何截获 Alice 和 Bob 之间通信的人只会获得_A_或B。而单独看这些点，它们毫无意义。

就这样，他们_安全地_创建了一个共享密钥！太棒了。只需记得保持生成的密钥安全！

遵循甘道夫的建议

承诺方案

好吧，我们知道如何安全地生成共享密钥。那我们还能做些什么？

另一个想法是_提前_对某个值进行承诺。为了说明这一点，让我们玩一些石头剪子布。但我们得轮着玩。这是玩法：

Alice 先出石头。然后 Bob 出布。这是他人生中最简单的胜利。

显然，这里的问题是 Alice_提前_暴露了她的手。有没有可能她可以_隐藏_自己的出牌呢？

一场不寻常的石头剪子布

Alice 产生一个与她的出牌（剪刀）_绑定_的值，但又能_隐藏_她的决策。这被称为承诺。之后，Alice_揭示_原始值，而 Bob_验证_它是否与承诺匹配。实际上，这就像把你的出牌放在一个密封的信封里，然后在需要时_打开_它。

我知道你们在想什么：为什么人们会以这种方式玩石头剪子布？我也不知道。但这不是关键 — 我们可以用这个想法来构建有用的协议。

创建承诺

让我们构建被称为Pedersen 承诺的方案。这种类型的方案需要一个_设置_步骤，它应该返回一个椭圆曲线的生成元G，以及另一个点H = [k]G。

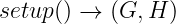
然后，如果 Alice 想要对某个消息_M_进行承诺，她按照以下步骤操作：

• 她将该值哈希为一个整数h(M)，
• 她然后选择一个随机整数r，也称为盲因子，
• 最后，她计算C = [r]G + [h(M)]H。这将是她的承诺。

承诺_C_可以与任何人共享，因为它是隐藏的：它不会透露关于消息的信息。之后，Alice 可以共享秘密值_M_和r，任何人（例如 Bob）都可以重新计算_C_并检查它是否与 Alice 共享的一致 — 我们说 Alice_打开_了承诺。

正式来说，我们说，承诺方案必须满足以下条件：

• 隐藏性：它不应该泄露关于承诺消息的信息。
• 绑定性：承诺只能使用原始_M_和_r_打开。否则，它应被视为无效。

那么，盲因子又是什么呢？如果我们不使用它，那么_C_将_总是_看起来像这样：C = [h(M)]H。这不是好事，因为哈希函数是确定性的：对于固定输入，它总会产生相同的结果。

因此，一旦你看到两个相同的承诺，你就会立刻知道它们是与相同信息相关的 — 如果你_已经知道_秘密数据，那么承诺根本不 是_隐藏_的！记住：

一条链的强度仅与其最弱的环相当

引入随机盲因子解决了这个问题。一般来说，引入随机性的想法用于防止基于重复的脆弱性，就像我们刚才描述的那个一样。

承诺方案是更强大结构的基石，我们将在后续文章中探讨。

签名

我们已经讨论过使用椭圆曲线的签名例子，称为椭圆曲线数字签名算法（或简称ECDSA）。但还有其他方法可以创建签名。

特别是，还有一种叫做Schnorr 签名的协议。说实话，它比 ECDSA 更简单。想想，或许我们应该先介绍这个，而不是 ECDSA。是的，抱歉。

抱歉，Harold

无论如何，Schnorr 签名通常以模 q 的整数的_加法群_呈现，但正如我们之前提到的，任何使用该群的构造都可以_适配_到椭圆曲线。我们现在将演示这一点。

设置与之前的 ECDSA 一样：Alice 持有一个私钥d，而 Harold（抱歉 Bob）持有关联的公钥Q = [d]G，其中_G_是 Alice 和 Harold 一起同意的群生成元。

签名时，Alice 进行以下操作：

• 她选择一个随机整数r，并计算R = [r]G。
• 然后，她计算哈希值e = H(R || M)。这里，_||_表示按位拼接 — 所以本质上她只是哈希一串零和一。同时，_e_是一个整数。
• 最后，她计算s = r - e.d。

签名是对(s, e)。要验证，Harold 按照以下步骤进行：

• 他计算R’ = [s]G + [e]Q，
• 如果满足e = H(R’ || M)，他就接受。

简单吧？这次，我们不需要计算任何模乘逆。而且检查_R’_是否应该与_R_匹配也相对简单：

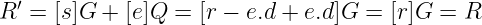
Schnorr 签名为更成熟的 ECDSA 提供了一种替代方案。实际上，它们更易于实现，不依赖于模乘逆，并且理论上提供了更高的安全性。一些区块链，比如Polkadot，已经采纳了这种签名方案；最终，使用什么由你来决定。

零知识证明

零知识证明（简称ZKPs）在过去几年成为热门话题。它们并不是什么新发现，但由于其性质以及可以利用它们做的酷事，受到了很多关注。

本质上，ZKP是一种证明_对某物的知识_的方式，而无需透露关于它的任何信息。听起来疯狂，对吧？我怎么可能告诉你我知道一些事情而不告诉你那是什么？

这是一个非常好的视频，展示了 ZKP 的一些精彩例子。

我最喜欢的一个例子是_沃尔多在哪里_的证明：我想证明的是我知道沃尔多在哪里。一种选择是直接指着他 - 但这会有效地揭示他的位置信息！

为了_不_揭示它，我可以这样做：拿一块大纸板，在上面打一个和沃尔多一样大小的洞，然后把它放在书上。你可以通过洞看到沃尔多，但你看不到他在页面上的位置！

他就在这里，这个滑头!

Schnorr 协议

显然，我们不会用椭圆曲线构建一个沃尔多位置证明系统。我们得满足于更简单的事情：证明对_一个点的离散对数_的知识。也就是，证明我们知道某个值x，使得Y = [x]G，其中_G_是椭圆曲线群的生成元。该群的阶数为n。

我们将描述的是称为Schnorr 协议的内容，适配于椭圆曲线。它是一个非常简单而优雅的协议，为更复杂的知识证明提供了良好的基础。

顺便说一下，这是Claus P. Schnorr，骄傲地度过他的80岁。真是个传奇。

协议流程如下：Alice，我们称之为证明者，想要证明她知道x。Bob，验证者，知道Y。当然，Alice 可以披露_x_的值，Bob 可以验证它是否确实是_Y_的离散对数（Y = [x]G）。但出于某种原因，假设_x_必须保持私密。

Alice和Bob按以下方式互动：

• Alice 首先选择一个随机整数r，并计算R = [r]G。这是一个承诺，然后她将其发送给 Bob。
• Bob 随机选择另一个整数c，并发送给 Alice。
• 然后，Alice 计算：

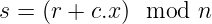
• Bob 接收到s，检查是否满足：

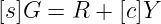
（我将把数学留给你去检查）

有趣的是，如果出于某种原因 Bob 仍然不信服，他可以向 Alice 发送一个_新的值_的c，并重复这个过程。事实上，他可以这样做任意多次，直到他满意为止。这暗示了一些密码协议是_交互式_的事实，我们稍后将在系列文章中回到这一点。

可验证的随机函数

我们还可以做的另一件有趣的事情是_以可验证的_方式生成随机数。

什么？

这个听起来疯狂。我相信一个比喻可能会有所帮助。

假设你购买了一张彩票。你去商店，选择一些随机组合的数字，然后收到相关的票。

然后，彩票获胜者被选中，恰好是你的号码！你怎么证明自己是赢家？当然，你有票！所以你只需把它呈现在彩票中心，你就能获得奖品！

运气真好！

虽然这个比喻并不完美，但它传达了一个重要的信息：可能关于随机生成的数字有一些证明。

可验证的随机函数（或简称 VRFs ）正是这样做的：它们生成一个基于用户某些输入的伪随机数，并提供生成过程是_诚实且正确_的 证明。我们将在后续文章中更详细地讨论这一点，所以现在，让我们专注于仅使用椭圆曲线实现 VRFs。

因此，创建 VRF 时的目标如下：Alice 想要_生成_一个伪随机数，让 Bob 能够验证。他们就一个订单为_n_的椭圆曲线生成元_G_达成一致，也达成对两个算法的共识：h 和 h’ 。前者与以往一样哈希到一个数字，而后者哈希为椭圆曲线上的一个点。

设置与通常的细微差别不大：Alice 有一个私钥 d，和一个公钥 Q = [d]G 。但这里有一个额外的元素：VRF 的输入 a 是 公开的 。每个人都将同一个数字通过他们各自的 VRFs 运行，并产生不同的输出。

现在，算法分为两个步骤：一个 评估 步骤，该步骤生成随机数及其证明，以及_验证_步骤。Alice 按如下方式执行 评估：

• 她计算 H = h’(Q, a)。这是椭圆曲线上的一个 点。
• 然后她计算 Z = [d]H ，即 VRF 输出 。
• 现在她需要生成一个证明。她选择一个随机数 r，并计算 U = [r]G 和 V = [r]H 。
• 她将_所有内容_哈希成一个数字c：

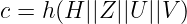
• 最后，她计算 s：

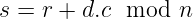
VRF 评估的结果是π = (Z, c, s)，其中_Z_是真正的伪随机输出，其他值则作为_Z_的正确性证明。

最后，Bob 需要_验证_证明。他这样做：

• 他计算与 Alice 计算相同的哈希，H = h’(Q, a)。他可以这样做，因为_Q_和_a_都是公开的。
• 然后，他计算_U’_和_V’_如下所示。你可以检查这些结果与之前的_U_和_V_是否相同。

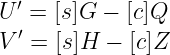
• 最后，他计算c’ = h(H || Z || U’ || V’)，并接受证明如果c = c’。

喔。好的。这真是一大堆东西。让我们梳理一下。

该输出_Z_由于哈希函数的性质是_不可预测_的，但它仍然是确定性的。正因如此，我们能够产生一个只能够在掌握私钥_d_的情况下运作的简短签名。

VRFs 的实用性可能不是立刻显而易见，但在适当的应用中，它们可能是一种强大的工具。例如，Algorand在其核心共识机制中使用 VRFs。谁知道你可能会为它们找到什么疯狂的应用！只要你拥有正确的工具，世界就是你的。

总结

如你所见，我们探索过的方法中，一些想法反复出现。在大多数情况下，我们执行两个操作，它们产出相同的结果。我们大多数时间都从_私钥/公钥对_开始。我们使用_哈希函数_将数据映射到感兴趣的集合。

将这些基本理念结合起来，可以构建出有趣和有用的协议，这就是这一切的全部。更复杂的应用可能需要更复杂的加密“游戏”。

当然，还有更多有趣的事情等着我们去做，使用椭圆曲线。例如，还存在更复杂的签名方案 — 如盲签名、环签名、阈值签名，等等。我们将在下一篇文章中介绍那些内容。

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～