密码学101：RSA算法解析

这是关于加密技术的一系列文章的一部分。如果这是你看到的第一篇文章，我强烈建议你从 系列的开头 开始阅读。

RSA 加密是目前使用最广泛的加密算法之一——它仅依赖于 模 n 的整数加法群。这是一个很好的例子，展示了在没有椭圆曲线或其他更复杂构造的情况下，可以做到多少。

这一段专注于解释 RSA 算法的工作原理和细微差别。

潜在问题

许多加密机制的工作原理是，除非你知道某个 秘密密钥，否则执行某种操作是非常困难的。在 加密 中，这正是这个概念：未加密的信息在不知道该秘密密钥的情况下是 不可解读 的。

那么，这是如何实现的呢？通过构建一个问题，除非你有一些额外的 秘密信息，否则这个问题是 非常难以解决 的。RSA 就基于这样的问题：将大数字分解为其素因子。即：给定一个（大）数字 n，将其表示为：

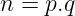
其中 p 和 q 是大素数。如果你知道 p 和 q，计算 n 是极其简单的——如果你知道 n 和 q，计算 p 也是如此。

多大算是足够大？

当然，如果问题容易解决，那这一切都是 毫无意义 的。例如，如果 n = 7×11 = 77，那么因式分解几乎在瞬间就完成了。然而，随着素数的增大，因式分解所需的时间也越来越长。

建议的素因子 p 和 q 的大小在 1024 到 2048 位之间。作为参考，这是一 个 1024 位素数的样子：

170154366828665079503315635359566390626153860097410117673698414542663355444709893966571750073322692712277666971313348160841835991041384679700511912064982526249529596585220499141442747333138443745082395711957231040341599508490720584345044145678716964326909852653412051765274781142172235546768485104821112642811

是的，它很大。

估计找到一个 2048 位长的大数的素因子需要多长时间是很困难的。主要是因为实际上并没有进行过这样的尝试！

但仍然有人推测，即使有强大的硬件，这也需要从 数百年 到 数千年。除非量子计算技术变得可用——这是另一个故事。

准备工作

我们如何使用前面的问题来加密数据？这样做将需要一些定义。特别是，我们需要了解 欧拉函数 及其性质。

欧拉函数

对于任何自然数 n，该函数（表示为 φ(n)) 计算有多少个小于 n 的自然数（不计算 0）与其 互质。

互质意味着这些数字 没有 共同的素因子。另外一种说法是，互质数字的 最大公约数 是 1。

例如 6 和 25 是互质的。

注意，对于素数 p，小于它的每一个数字都是 互质 的（因为 p 是素数，它唯一的素因子是 p！）。所以我们可以写为：

同时，对于 n = p.q，如果 p 和 q 是素数，则有：

一个重要特性

我们为何关心欧拉函数？主要是因为 欧拉定理，它指出如果 a 和 n 是互质的，则有：

如果我们两边都乘以 a，就会得到：

显然，有一个神秘的数字 φ(n) + 1，似乎可以让我们恢复原始值 a！

我想我知道这将向哪个方向发展……

算法

如果我们在之前的方程中将 a 替换为我们的消息 m，那么我们就得到了一个很好的加密机制的基础，因为我们对 m 有一个操作，可以让我们 恢复 m！

我们需要做的是将这个过程分为 两个步骤。为此，我们简单地 因式分解 φ(n) + 1。

不过这不是你平常见到的因式分解。真实情况是，我们选择一个某种 随机的 大数字 e，前提是 e < φ(n)，并且 e 与 φ(n) 互质。然后，我们计算另一个数字 d，使得：

这实际上只是 e 的模 φ(n) 的乘法逆元。

并且以这种方式计算 d，确保了以下命题成立（这相当简单可以证明，所以我将这项任务留给你）：

有趣的是，通过 e 和 n 的知识，很难计算 φ(n)，因为为此你需要 n 的素因子！这实际上是一个非常困难的问题！出于这个原因， e 可以公开发布——并确实是在 RSA 中的 公钥。

步骤

剩下的就是分为两个步骤。我们使用公钥 e 来计算一个 密文：

在不知道 d 的情况下，这不能转换回 m。因此，只要 d 保持秘密，那么只有持有这个值的人才能解密 c。正因为如此， d 将成为我们的 私钥。

要解密，我们简单地执行以下操作：

于是，消息被解密了！

注意，你还可以使用此方案进行数字签名，使用 d 生成签名，使用 e 验证签名。很酷吧？

总结

这就是 RSA 加密的工作原理。

邓布利多表示赞同

关于它没有更多要说的了。不过，还有几个点我们没有涉及——也就是如何 计算模乘法逆元，或者如何 生成大素数。我们在这里不会涵盖这些，但当然，它们也是 RSA 加密的重要组成部分。

然而，在 RSA 中有一些特别敏感的点，可能成为整个密码系统的巨大陷阱，奇妙之处如 这里 所解释的那样。理论上相当完善，但自己实现这个看似简单的方案可能会使之非常脆弱。

邓布利多感到震惊

这就是 RSA 被广泛认为已过时的原因之一，并已被大多数应用中的 椭圆曲线密码学 (ECC) 取代。

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～