密码学基础：配对应用及其他

这是关于加密的文章系列的一部分。如果这是你第一次看到的文章，我强烈建议你从 系列的开头 开始。

在我们 前一篇文章 中，我们了解了 pairings，这一结构开启了一些新的可能性，并且基于 identity 的一些独特加密方式。而我们也看到了 基于身份的加密 ( IBE ) 是如何工作的。

这次，我们将聚焦于更多的 pairing 应用示例，同时在这个过程中也会添加一些其他细节。

和上次一样，pairings 将被视为某种 黑盒，因为我们不关心如何计算它们——我们只会关注它们的 双线性 属性。

所需设置

对于我们即将介绍的方法，必需有一定的设置或基础设施。这在 上次文章 中已经介绍过，但为了自成体系，这里我们将简要重申这个想法。

假设存在一个 私钥生成器 ( PKG )，负责从用户的 身份 中生成私钥，同时需要公开一些 系统参数。你可以查看 前一篇文章 以了解其工作原理和参数。

不再多说，我们开始吧！

密钥交换

如果你一直在关注这个系列，这听起来可能会很熟悉——因为我们已经在这个系列中 看到过 密钥交换方法。Diffie-Hellman 密钥交换 (DHKE) 算法是加密中的基本方法之一，对于任何使用对称密钥的场景至关重要。

自然，这是开始我们 基于身份的加密 之旅的好地方。

为了实现这一点，我们需要一种 特定 类型的 pairing ——有时被称为 自我-pairing。我们在 上一篇文章 中讨论过这个概念。不过，这里的思想简明易懂，可以在这里重复一下：我们不再假设输入来自两个不相交的群体，而是允许它们来自 同一组：

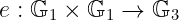
要使这成为可能，必须满足某些条件，但我们不必过于担心这一点，姑且假设这是可以做到的。为了我们的 sanity。

生成密钥

一旦我们手中有了 自我-pairing，密钥生成就相当简单。假设Alice (Alice) 和Bob (Bob) 想要生成相同的共享密钥。而他们已经获得了他们的 秘密钥匙：

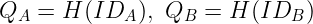
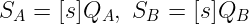
策略很简单：如果我们可以找到两个 pairing 评估得出相同的结果——并且可以由Alice和Bob独立执行，那么我们就成功了。看看这是多么优雅：

或者简单地说：

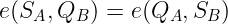
Alice只需知道她的秘密钥匙和Bob的公钥，她就可以计算左侧的表达式。相反，Bob只需要Alice的公钥和他的私钥，他可以计算右侧的表达式。两者都得到相同的结果！真是令人惊叹。

扩展方案

迪菲-赫尔曼协议 可以扩展，使得多个参与者之间可以生成共享密钥。所以，假设我们有三个参与者想要生成相同的共享密钥。在处理椭圆曲线时，他们将计算这个共享值：

假设Alice有秘密值 a，Bob有秘密值 b，查理 (Charlie) 有秘密值 c。

一个 类似的想法 可以应用于 pairings，这个想法在2003年由 Antoine Joux 提出。查看下列 pairing 评估：

我们可以巧妙地分配指数：

你看，这里有趣的是值 [a]G，[b]G，和 [c]G 并没有泄露关于秘密值 a，b，和 c 的信息（除非你能解决 DLP！）。因此，这些值可以被 公开，然后，每个人都可以计算出相同的共享值！

这个扩展并未在该过程中使用用户的 identity。这反过来又表明， pairings 使得 基于身份的加密成为可能，但并不 局限于此应用。

就这样！基于 pairings 的密钥交换。不错吧？

pairings 开始看起来吸引人，是吧？

基于身份的签名

如果基于 pairings 的加密是可能的，那么下一步就是尝试基于它们构造 签名。

我们将呈现一个 简单版，这将相对容易理解。还有其他有趣的签名方案——例如著名的 BLS 签名，但我们不会详细讨论，以避免信息过载。让我们保持简单。

致死原因：加密内容堆砌

简化版

我们再次需要正确定义设置。请稍等一下！

其开始过程与之前相似，我们有一个带有主秘密 s 的 PKG，公示值 P 和 Q = [s]P。此外，我们还需要几个哈希函数：将之前文章中定义的同一个 H 称为 H₁：

还有第二个哈希函数 H₂，必须是以下形式：

最后，我们假设签名者获得了以下形式的私钥：

哈希的 ID 是 公钥。这就是我们所需要的全部！

设置完成后，让我们看看 基于身份的签名 (IBS) 是如何工作的。

顺便说一下，所呈现的方案是基于 这篇论文。

为了对消息 M（任意长度的位序列）进行签名：

我们需要做以下事情：

• 首先，签名者采样一个随机数值，一个整数 k
• 然后，他们继续计算值 U 和 V，如：

这些值将是 生成的签名，元组 (U, V)。这个结果与 椭圆曲线数字签名算法 (ECDSA) 的结果非常相似，其中一个结果编码了随机数，另一个编码了私钥。或者，可以说，一个是 挑战 ( U )，另一个元素就充当 验证者 ( V )。

我们也可以将 V 理解为某种 知识证明，即证明掌握了秘密钥匙。

剩下的就是 验证。到目前为止，我们并没有使用 pairing——所以你可能会发现这正是它们在这个框架中适用的地方。实际上，想法是进行两次不同的评估，一次使用 U，一次使用 V。如果这些评估结果匹配，则这将意味着 V 是正确计算的——这表明签名者持有正确的 私钥。

这些评估为：

很容易检查这两个表达式的计算结果应该是相同的：

如你所见，如果 V 是正确的，并且确实使用了主秘密 s，那么这些方程应该成立！否则，我们就必须找到一个有效的 V，使其满足上述等式——这应该是 超级困难。

从正式上来说，这被称为 双线性迪菲-赫尔曼问题 (BDHP)，这是这些基于 pairing 的方法安全性的基础。

我的意思是，这 有点 疯狂——但同时也 并没有那么疯狂。尽管 pairings 相当复杂，但我们的构造似乎并不复杂！我们已经见过更复杂的协议 在这个过程中。我这样说是为了尽量破解基于身份的加密：它确实是复杂的，因为 pairings 是复杂的，但如果我们忽略它们计算的细微差别，仅仅关注它们的 属性，事情就会变得清晰得多。

哦，我兴奋得难以自已

总结

正如你所想象的那样，pairings 可以做其他许多事情。按照 这篇文章 中建立的蓝图，我们可以推断出有多种方式来构建 承诺方案，知识证明，不同类型的 签名，VRFs，以及其他基于 pairings 的原语。

然而，我建议慢慢来，以便你有时间理解我们所探讨的这一新 pairing 内容。

我们看到了在 基于身份的加密 领域的一些应用（这非常有趣，因为我们不再需要记住那些麻烦的长公钥），同时也注意到 pairings 还有其他应用。

为了进一步巩固这个想法，下一次我们将关注一个特定的 承诺方案，这对于我们理解一些现代的 零知识证明 非常重要。下次见！

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～