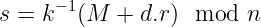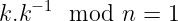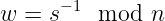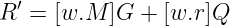密码学基础：加密技术与数字签名解析

这是关于密码学的一系列文章中的一部分。如果这是你看到的第一篇文章，我强烈建议你从系列的开头开始阅读。

在上一篇文章中，我们通过定义椭圆曲线群扩展了对群的基本知识。我们简要提到这些概念将使我们能够构建一些有用的密码机制。

正如我们所承诺的，我们将查看两个这样的基本技术示例：一个用于数字签名，一个用于加密。但在此之前，我们需要定义几个在我们开发中至关重要的工具。我们将以椭圆曲线为背景，但这些概念可以推广到其他群。

你可能听说过私钥和公钥。让我们看看它们到底是什么。

密钥与离散对数问题

学习数字签名时通常讲述的故事是这样的：一个用户（假设是Alice）用私钥（或秘密）可以签名一条消息，然后任何人都可以用相关的公钥验证该签名。

是的，太棒了

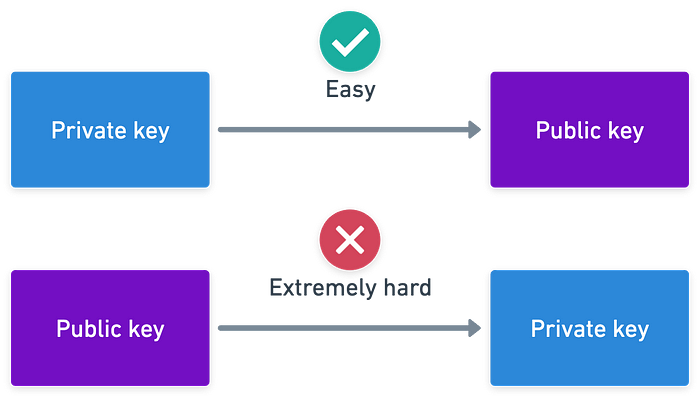
当然，我们对这一机制背后的原理一无所知。但其中有一个隐含的信息：从公钥获取私钥是不可能的，因为这意味着任何持有Alice公钥的人都可以以Alice的名义生成签名（毕竟它被称为私有是有原因的）。考虑到这一点，让我们看看这些密钥到底是什么。

还记得第一篇文章中的群生成元吗？好吧，这就是它们的用武之地。椭圆曲线作为群，也有生成元和子群！

假设Alice和另一个人Bob在椭圆曲线上达成一致，选择一个生成点G。然后，Alice从模 q 的整数集合中选择一个随机数d，使得d < q。此外，假设d是一个大数，而不仅仅是 12 或 35。这将是她的私钥。

被抓了

Alice接着计算Q = [d]G，利用点倍增的力量，获得群中的另一个点——这将是她的公钥，她可以安全地将其发送给Bob。

显然，Q编码了关于私钥的信息。Bob可以尝试计算一个数字d，使得Q = [d]G——但问题是，如果我们的椭圆曲线群“足够大”，这将花费Bob非常非常长的时间。这正是秘密所在：即使知道Q和G，找到d也应该几乎是不可能的。这被称为（某种形式的）离散对数问题（DLP）。

当然，如果我们的群恰好有 1000 个元素，或者Alice选择的数字是“较小的”，那么尝试可能的d值是一个可行的任务。你可能可以写一个脚本在 10 分钟内解决这个问题——这被称为暴力破解。当我们有巨大的群时，DLP 问题才真正显现出其优势。例如， 曲线 25519 的子群阶数大约在~2²⁵⁰左右。这是一个相当大的数字。祝你好运，试着暴力破解d。

加密

Alice现在持有一个数字d作为她的私钥，而Bob持有相应的公钥Q，这只是椭圆曲线上的一个点。他们可以用这个做什么？

我们开发的这些工具刚好足够开始构建有趣的东西（耶！）。让我们加密一些数据！

想象一下，Bob想要保护一条消息，使得只有Alice能阅读。如果他们是学校里的青少年，他们可能会用一种秘密代码交换书面消息，只有Alice和Bob能理解。由于他们都知道秘密代码，他们都可以“解开”编码——所以这被称为对称加密。

好的，听起来简单！

在实际应用中这是如何发生的？想想看：任何消息只是一堆零和一，一些二进制数字。如果我们扭曲这个数字，我们实际上将其转换为无意义的乱码——这通常被称为密文。如果我们以可逆的方式做到这一点，原始消息就可以恢复！

就像魔法一样

这里有一个简单的实现 ，如果你想玩玩。

为了澄清，这里的可逆性是通过逻辑异或操作提供的。别担心——关键是我们能够用共享的秘密密钥来掩盖原始消息。

那么椭圆曲线呢？

显然，我们在之前的构造中并不需要椭圆曲线。这表明密码学远比单一工具要广泛得多，而且实际上早在椭圆曲线出现之前就已经存在。

但秘密密钥发生了什么？Alice和Bob如何达成共享密钥？如果他们以不安全的方式这样做，那么其他人可能在监听，而那个第三个人（假设是查理）就可以读取Alice和Bob的秘密消息！这可不妙，我们的加密变得毫无用处！

我们还不必惊慌。尽管有方法可以安全共享秘密密钥 ，但还有另一种解决方法：我们可以使用椭圆曲线以非对称的方式获得共享秘密。

非对称加密

假设Bob想要为Alice加密一条消息M。Alice可以简单地选择一个私钥d，并将她的公钥Q = [d]G分享给Bob，而不是达成一致的密钥。在这种设置下，我们可以设计一种方法，让Bob只为Alice加密消息。这是具体步骤：

• 他选择一个随机数k < q，通常称为随机数，
• 然后Bob计算[k]Q，并用它来计算一个掩码，我们将其表示为P，使用一些商定的算法，
• 他使用异或掩盖消息，如前面的例子，并获得密文C = M + P，
• 最后，他计算[k]G，其中G是Alice和Bob之前达成一致的群生成元，
• Bob然后将点对([k]G, C)发送给Alice。

Alice知道私钥d，可以执行以下操作：

• 她计算d。我们没有提到这一点，但在椭圆曲线中乘法是交换的，所以d = k = [k]Q。在不知道k的情况下，我们仍然可以重建Bob使用的掩码。太神奇了。
• 使用商定的算法，Alice计算掩码，并用M = C + P反转掩码。

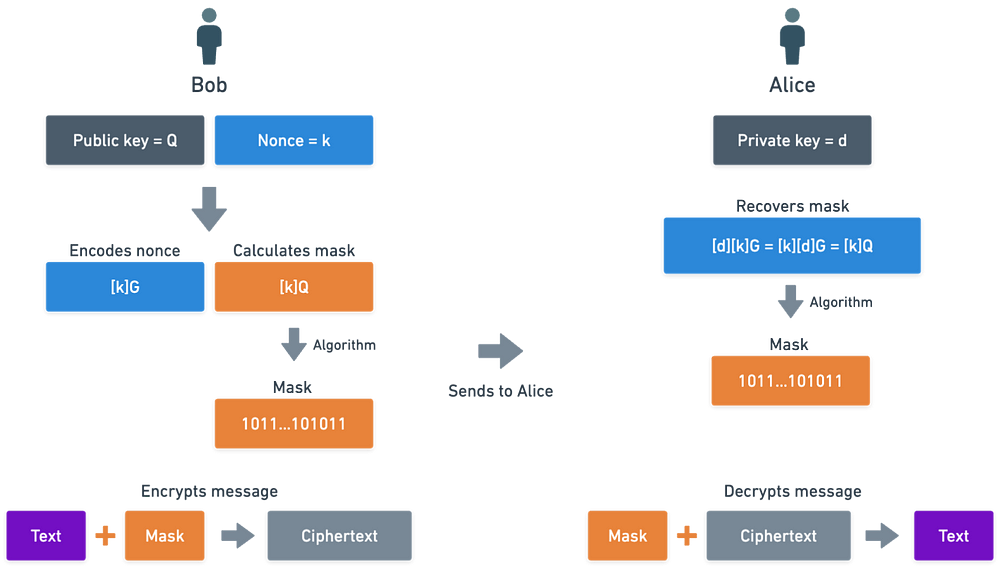
视觉效果往往很有帮助。总的来说，过程看起来是这样的：

ECIES 在行动

这个过程被称为 椭圆曲线集成加密方案，简称 ECIES。还有其他类似的方案，例如 ElGamal 加密系统 ，可以适应椭圆曲线。

我不知道你怎么想，但我觉得这很吸引人。通过仅仅几个操作，就可以以一种在实践中“无法解读”的方式保护数据，而这种方式只有一个“数字”（只有Alice知道）。

我们对群的理解终于开始获得回报！

总结：

这种加密方法通过计算一个掩码并将其添加到原始消息中来工作。

在对称加密中，双方都需要知道掩码；在非对称加密中，只有一方知道私钥才能解开掩码。

数字签名

加密假设编码的信息“必须对未授权的读者保密”。这并不总是正确的：有时信息可以是“公开的”，但我们关注的是“证明其真实性”。例如：

假设Bob想向Alice发送 1000 美元的付款请求。他向Alice发送他的银行账户号码和他需要转账的金额。如果其他人（比如查理）拦截了消息，并更改了Bob的银行账户为他的账户，会发生什么？

Alice无法检查这个银行账户是Bob的还是查理的。我们能做些什么来防止查理利用这个策略来盗取钱款？

如果Bob能够以某种方式“签名”信息，那么Alice就可以检查签名是否“有效”，并接受该消息。反过来，如果查理更改了银行账户，那么签名就不再有效，Alice将拒绝该消息。这正是“数字签名”所提供的功能。

我们现在要介绍的是“椭圆曲线数字签名算法”，简称“ECDSA”。这个过程可能比加密稍微复杂一些。它将涉及一些新的数学技巧。我们将在需要时定义它们。请耐心等待。

• Bob像在加密示例中那样编码他的消息，但这次输出是一个“整数”M。我们稍后会看到如何做到这一点。
• 然后，Bob选择一个随机数“k”，就像在加密的情况下那样，
• 他还计算“R = [k]G”。我们用字母“r”表示“R”的 x 坐标，
• 他进行的最后一个计算是数字“s”，计算如下：

• 最后，他将对（r，s）对发送给Alice。

计算 s 中的 k⁻¹不是k 的倒数（即，它不是 1/k）。

相反，k⁻¹表示模乘逆 。本质上，它是一个数字，当与 k 相乘时，产生以下结果：

此外，模数（n）是一个特殊的数字：它是生成点 G 的阶。椭圆曲线上的每个点都有一个阶，这是使[n]G = O 的最小整数。这也是群_𝔾_的阶。

好的，这些内容有点多，但我们得到了签名。剩下的就是“验证”它。由于消息是公开的，Bob可以将其“编码”为Alice使用的相同数字“M”。然后，他按照以下步骤进行：

• 他计算“w”作为“s”的模逆

• 然后，Bob取这个值并计算：

• 如果“R’”的 x 坐标与值“r”匹配，他就接受签名。

计算数字并检查“R’ = R”是读者的一个不错的练习。如果你打算尝试，只需记住，由于“G”是阶为“n”的生成元，因此“[n]G = O”。你可能还需要使用一些模算术性质 。

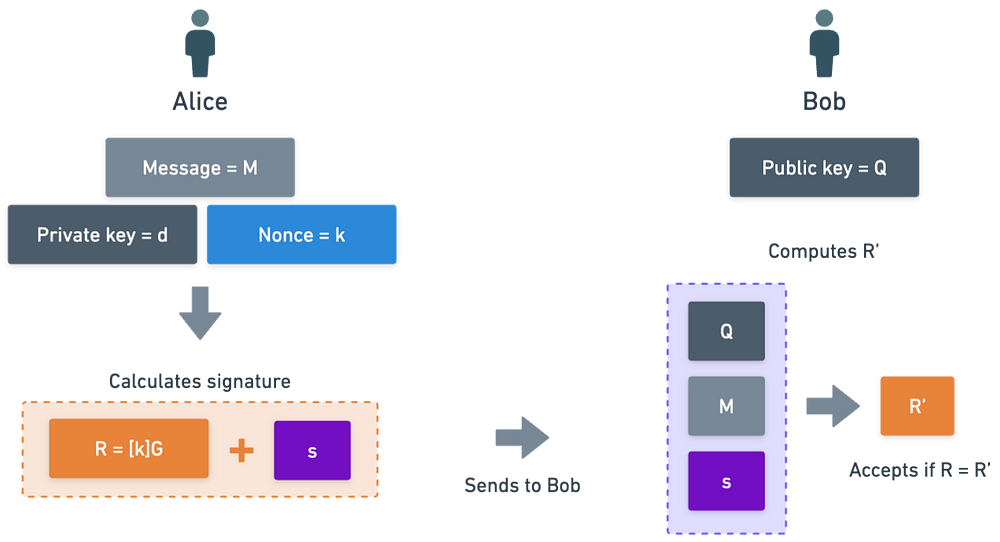
ECDSA 的实际应用

再一次，就像魔法一样，签名实际上只是一个“数字对”！这里的想法是，计算“s”在知道私钥的情况下非常简单，但在不知道的情况下非常困难——你必须解决一个 DLP 问题！

如果查理想要更改消息，他别无选择，只能“暴力破解”。我们知道这对他来说会怎样（剧透：这不会有趣）。

让我们再说一遍，以便记住：

签名涉及计算一种“挑战”R 和一些“验证密钥”s。对（R，s）构成一个签名。

值 s 是特殊的，因为当与公钥 Q 和原始消息 M 一起放入搅拌机（即某个过程）时，它会返回挑战 R。其想法是，s 只能在知道私钥的情况下计算。

总结

在接下来的几篇文章中，我们将探索更多的技术和构造，但现在这是一个很好的停顿点。

我认为理解每一个数学或每一个计算并不是那么重要，而是要欣赏最终加密和数字签名实际上都是巧妙利用椭圆曲线操作，利用 DLP 问题的力量。

好消息是，我们目前拥有的工具可以做很多事情。更复杂的技术将需要引入一些新的和更复杂的概念——我们暂时不去探讨。

此外，还有一些事情我们尚未解释，比如在数字签名的情况下“如何将消息转换为数字”，以及在加密的情况下“如何从椭圆曲线中的一个点获得掩码”。

这可以通过“哈希”来完成，这是一种非常强大的工具，将是下一篇文章的核心主题！