密码学101：全同态加密

这是关于加密技术的一系列文章中的一部分。如果这是你看到的第一篇文章，我强烈建议你从本系列的开头开始阅读。

我们到了。旅程的最后。

在这一路上，我们学习了很多。最初的简单内容介绍变成了一系列完整的文章，我们探讨了许多加密领域的基础概念，以及一些非常接近先进水平的技术。我对此结果感到非常高兴。

然而，还有一个重要的话题我们至今未涉及。它可算得上是加密技术的一个圣杯。而现在，我们已经具备了理解现代技术如何解决这个问题的所有工具。

没错。是时候深入探讨_全同态加密_了。

继续吧，我忠诚的坐骑！

引言

同态 是一个我们应该已经熟悉的术语，因为我们专门撰写了一篇完整的文章来解释它的含义。不过，简短的复习总是有益的。

同态是一种函数，它具有一个简单的特性：

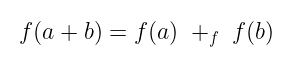
请注意操作不必是相同的这一微妙区别。

用简单的语言说：先将输入相加然后再应用函数的结果与先应用函数再相加的结果是相同的。

确实，我们说这个函数是相对于某个操作是同态的，在上述场景中，这个操作恰好是加法。

一些同态也可以是可逆的，这意味着，对于某个功能值 y = f(x)，存在某个逆函数使得：

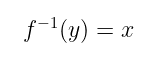
在这种情况下，这个函数称为同构。

某些加密函数的行为类似于同构。能够_还原_加密是功能的要求，但其作为同态的表现则解锁了一些新的超能力。

具体来说，你可以对加密值进行加法，并确保在解密时，得到的结果与先对未加密值进行加法的结果相同。这非常酷——它允许应用程序对加密数据执行操作，从而保持隐私。

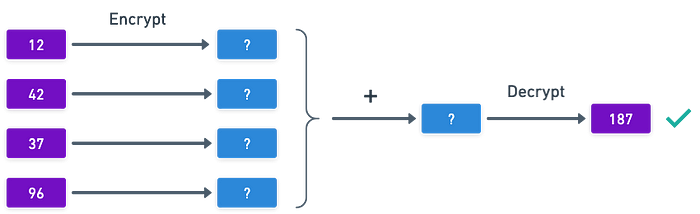
不过有个前提：在操作群体时，我们只能支持一种操作。

因此，我们可以创建基于群体的加密方法，这些方法可以相当轻松地处理加密值的加法（即ElGamal）。但是你想要乘法？不行。没法做到。

支持乘法是重要的——正如我们在简短的算术电路讨论中看到的，我们可以通过加法和乘法门计算几乎任何东西。这意味着，如果我们能够支持这两种操作，那么我们可以在加密数据上执行任意计算，同时保持数据隐私！

支持单一操作的算法家族被称为部分同态加密，或称PHE。

重要的是，这可能对某些类型的应用足够。例如，如果我们只需要保持加密余额并进行加法或减法，则我们不需要完整的FHE能力。

事实证明，支持加法和乘法的方法并不容易构思。很长一段时间，这对研究人员来说仍然是个难题。像Boneh-Goh-Nissim算法这样的努力基于配对，能够处理单一乘法。

这根本不够。支持两个操作仍然是遥不可及的。

但等等…… 两个操作？我们知道一个更好的结构！

通过环(Rings)进行加密

环听起来就像_全同态加密_应自然支持的代数结构。像NTRU这样的努力最初被提出，但只能处理_有限数量_的乘法。这是有充分理由的。

在上一篇文章中，我们研究了Kyber，它可以用来加密短消息。当我们查看解包步骤（想想解密），我们观察到恢复的消息并_不完全_是原始消息。

但它距离原始消息接近。只相差一个小误差。只要保持这个误差小，解密就会成为可能。

这就是一般所称的适度同态加密（SWHE）的思想：这意味着，当误差保持较小的时候，方法可以处理解密。

尽管Kyber不是一种同态加密方法，但思想大致相同。

乘法有让_误差膨胀_的趋势，这就是环基方法无法支持无限量乘法的原因。至少直到出现了一些更为显著的事件……

在_2009_年，Craig Gentry发表了他的博士论文，介绍了一些新的技术，从而解锁了第一次真正的_FHE_方案。

正如他的原始工作所示，研究从一个初步构造开始，在此之上应用了某些技术，将他的基本SHE方案转变为FHE。我认为在这里最好的方法是遵循相同的步骤！

基础构造

一切始于对适当的环的选择。我们将处理形式为𝔽 [X]/(f(X))_的环。同时我们也需要上述环的 理想(ideal)——请记住，理想(ideal)是 R 的一个子集，它在加法和乘法下是封闭的：

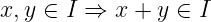
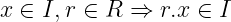
理想是_随机生成_的。我们抽取一个系数小的随机多项式 g(X) ——然后，理想就是 (g(X)) ，就像我们在这里中解释的那样。

接下来，我们需要再次讨论_基_的概念。我们在几篇文章前简要提到过这个概念。简单地说，基由一组_独立向量_组成，通过_线性组合_可以生成格点中的任何点。我们说一个基_生成_了一个格子Λ。

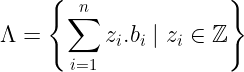
格子的基不是唯一的，我们可以选择多种有效的基。正如我们在上一篇文章中提到的，有_好基_和坏基——好的基允许我们快速解决最短向量问题，而坏基，即使生成同一个格子，也不适合有效地解决它。

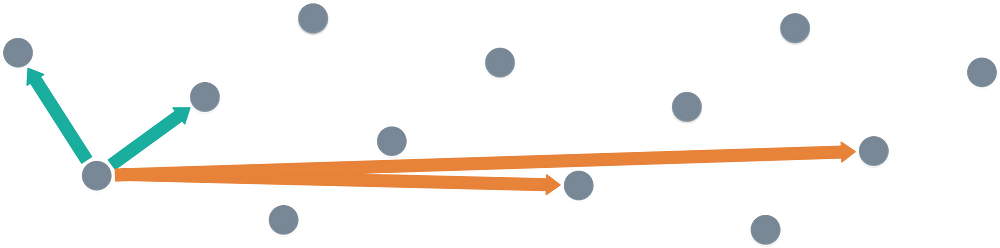
一个好基（绿色）与一个稍微差的基（橙色）。

从图中，我们可以想象，一个好基应该是一组短的、非共线（如果可能的话是正交）的向量。另一方面，坏基则恰恰相反：长的、共线的向量。

因此，在我们即将关注的构造中生成了两个基——它们作为加密过程中的_秘密_和私钥：

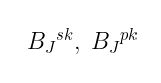
秘密钥是一组“好”的基，而公开钥则是一组“坏”的基。

应该注意的是，这里我们提及的是理想J，而不是I。这不是错字——这背后是有充分理由的。我们慢慢来处理这个问题。

实际上，所有发生的事情就是，坏基仅适合计算加密值，但在解密时效率低下——而好基则在解密期间允许快速计算。对于我们来说，这里的细节已经足够——还有其他更迫切的概念等待我们理解！

加密

与往常一样，加密始于一个消息。我们常常避免明确定义的一个重点是有效消息属于哪个集合——换句话说，有效_明文空间_是什么。在我们的情况下，有效的明文值将属于商环R/I。这里有两点值得注意：

• 我们需要一种将消息编码为环元素的方式——但我们现在可以跳过这部分。
• 我们还需要理解_R/I_的一个元素是什么。稍后再对此进行更多讨论。

接下来，同样如常，我们需要在我们的加密方案中引入一些随机性。这确保了当相同值_m_被加密两次时，我们得到两个不同的结果。

从理想_I_中选择一个随机随机数，利用基Bᵢ。得到的密文_ψ_将是原始编码消息_m_加上随机数nonce i：

使用环特定语言，请注意m + i 本质上是余因子 m + I 的一个随机元素——即，所有具有如下形式的R中的元素：

如果这看起来令人困惑，那是因为它_确实_困惑。既然这是这一系列的最后一节，我将尝试通过几个例子更详细地解释这个问题。

视觉辅助工具的救助

假设我们正在处理环 ℤ[X]/(X²+1)。该环中的每个多项式的度数最大为 1——这意味着我们可以将多项式系数在一个_平面_中表示，作为_二维_向量。

第一个坐标对应于常数项，第二个坐标对应于一次系数（乘以x的数值）。

然后我们选择一个理想_I_的基 Bᵢ ——也就是，两个确定理想的向量。假设我们选择多项式 x + 2 和 2x - 1 ；我们可以将它们与二维空间中的向量 (2,1) 和 (-1,2) 关联起来：

灰色的格点和绿色的基向量。

基的选择隐藏了一个有趣的微妙细节。第二个元素的计算是 x(x + 2) = x² + 2x。但在我们正在使用的环中，x²等价于-1！

乘以x具有在环中旋转向量的良好特性。这就是我们得到一对良好的正交向量的原因。

图中每一个点（包括浅灰和深灰色的点）都是环 _ℤ[X]/(X²+1)_中的一个元素。很容易看到理想在这里的作用：并非每个点都包含在理想格中。

为了更好地理解余因子，只需采用不同的初始点，并使用相同的基向量生成一个格子：

绿色为旧理想格，新理想格为红色

你看到刚刚发生了什么吗？我们本质上得到了相同的模式，但_移位_了。这些就是我们所说的余因子。有趣的是，每个余因子可以通过其中的一个元素来识别——之后，所有其他元素都通过加上_基向量的线性组合_生成。

事实上，商环R/I由这些不同的余因子构成。只需一个单一代表就足以识别整个余因子，这也是一个等价类。

最后……对 Bᵢ 取模意味着什么？其实相当简单：我们环 _R_中的任何向量都可以表示为基向量线性组合的和，加上一个额外的短向量，使我们离理想“远点”：

绿色为基向量的线性组合，蓝色为额外向量。蓝色的点都是等价的。

我们可以把蓝色向量看作一个 余数 ，因此是对环中的任何点进行 Bᵢ 取模的结果。但它也是 余因子的一个代表！

从正式上来看，在环 R 中的任何点进行 Bᵢ 取模，将其映射到 R/I 中的相应等价类。因此，这两者是等价的：

余因子的代表通常为政策确定的基本平行六边形的元素，基准线在上图中为绿色虚线。

这不应该是太陌生——这与我们为模_q_的整数环描述的情况本质上是相同的：

为了巩固这一思想，看看当我们对上一个例子的所有余因子上色时会发生什么：

每个元素在ℤ mod q中恰好映射到R/I中的一个不同余因子，正如我们在灰色框中看到的——而q=5，即不同余因子的数量。

太好了！我们到目前为止的感觉如何？

*精神崩溃*

好消息是，理解这些概念后，我们至少可以解释加密和解密过程！

让我们再次关注加密函数：

我们现在能解释一些事情：

• m 代表 R/I 中的一个余因子。
• m + i 只是同一余因子的另一个代表。我们可以清楚地看到明文空间应该是 R/I。
• 然而，对 Bⱼ 取模稍微改变了一下事情：结果将是 R/J 的余因子代表。

我们还没有讨论 J，对吗？

理想 J 与 I 不同，以使得任何 J 的基与 I 的基结合使用可以得到 _环R 中的 任何元素。这有时表示为 I + J = R ，我们说 I 和 J 是 互质的 。

因此，i（本质上是 I 基向量的线性组合）在很大程度上 _向_m_添加了一些噪音。我的意思是，这两个表达式通常不会产生相同的结果：

我们会在后面看到这一点。

解密

解密密文 ψ 就像做几个模操作：

不那么简单的是理解 为什么。让我们暂时关注最简单的场景：

没有添加噪声。

同时，让我们假设 J 的两个基是相等的，看看再次发生什么，我们再举一个例子。

取一个消息 m 在 I 的 基本平行六边形 内部（由基向量定义的形状）：

I的基本平行六边形在绿色中，这个消息在其中。

因为_m_在_I_和_J_的基本平行六边形之内，所以在加密和解密过程中取模肯定会还原为m。但是如果J“更细”呢？

_J_的平行六边形比I“细”，J = (4 + x)

请注意，进行第一次模运算会将消息映射到_R/I_的新余因子——这是我们所不希望的！如果发生这种情况，我们在解密时就会得到一个不同的消息。因此，我们要求_J_在某种意义上要比_I_更粗。

现在，让我们向原始消息添加一些噪声 i，并使用我们的原始 J。如果在这种情况下进行一次完整的加密/解密循环会发生什么？

(1) 添加 m + i, (2) 对Bⱼ取模并得㐰出密文, (3) 对_Bᵢ取模并完成解密

正如你看到的……我们没有得到原始明文。

真的？

这里有什么问题吗？

实际上，我们刚刚见证的正是_全同态_这一切的核心：我们的误差 太大 了。如果我们保持小一点，事情会顺利相处：

显然可以看到，解密恢复了相同的值。

在加密过程中，我们很可能会得到一个在由ψ表示的J的余因子中的元素。我们并不在乎它在基本平行六边形内部，只要这个值代表同一余因子。同时，这与为什么我们使用两个基密切相关！

太好了，这样就确定了：只要噪音小，我们就可以解密，没问题。但请记住，本文不仅仅是关于加密——而是关于全同态加密。当我们开始执行一些操作时会发生什么？

同态操作

为了让方案全同态，我们必须能够同时支持 加法 和 乘法 。它们大致按以下方式工作：

加法期间总的噪音似乎会以可控的方式增长，但乘法却会让噪音迅速膨胀。这使得事情变得复杂：这意味着在进行几次乘法后，误差可能会增长到无法再解密的程度。如现在所述，这是一种_适度同态加密_方案——它能处理最大操作数量。

从理论上讲，它仍然“比这项技术之前的大多数努力好”，因为它可以处理的不仅仅是一次乘法！

好像事情还不够复杂……哦，天哪。

请保持耐心！

控制误差

执行操作时，误差无论如何都会增加。这是一个似乎超出我们控制的参数——可以说是方案的内在属性。

但我们可以做某些事情来保持他们在可控范围内。这正是Gentry论文背后的思想：一个可以在误差几乎太大的时候进行_刷新_的方案，从而获得更“短”的误差。

显然，如允许我们_解密_消息，那么误差就会消失——你只需选择一个新的小噪声向量。但当然，这件事的核心是要做到不解密。事情在这时变得有趣。用Gentry自己的话说：

“我们确实在同态上解密了密文！”

这是什么鬼？

我知道，这听起来疯狂！若要给出一个大致的想法，让我们称加密函数为𝓔而解密函数为𝓓。解密密文时，我们当然期待恢复原始消息：

如果我们在两边应用加密函数：

这就像解密然后重新加密——除非在某种意义上可以用_加密解密密钥_进行𝓓评估，从而获得新的刷新的密文。

我们怎么能实现这一点？

解密的戏法

这里的关键思想是将解密过程视为电路评估，类似于我们在几篇文章前所研究的。它只是一系列简单的操作，最终结果为原始明文（模I）。

通过这一点，我们可以利用我们的方案允许某些对密文进行操作（它是部分同态）。只不过这次是用_加密的密钥_代替实际的秘密密钥！

就像在密封盒子里解决一个拼图。有那么一点。

这个过程称为自引导。要让你相信所有这些花招是有效的，最好的方法是通过一个简化的例子。回到画板前。

设：

我们也选择一个_non-basesnow，作为秘密钥向量的线性组合：

可视化为：

明文域为绿色，秘密钥为橙色，公钥为红色

首先对几条消息加密。

假设m₁ = (1,1)，m₂ = (0,2)。当然，它们相加应该得到(1,3)。我们期待我们的方案在解密时返回此值。

在添加一小噪音后，我们得到了密文，结果为向量_ψ₁ =(5,2)_和ψ₂ =(4,3)。我们应该能够对它们进行加法，结果应解密为m₁ + m₂。

加密和同态加法。

接下来进入有趣的部分。我们需要加密秘密钥，因此我们向每个向量添加一些噪声i（它不必与之前的相同值相同），并按照公钥对这些结果进行映射。我们得到_ k₁ =(10,-1)和 k₂ =(6,7)_作为秘密钥的加密值。

为了简单起见，我选择了适当的噪音，以便结果已经成为公钥的基本平行六边形的一部分。

加密的秘密密钥。

接下来，我们想执行这个_同态解密_的事情。其思想是将密文映射到密钥域，但要加密。这样做将得到(12,1)——我们的刷新密文！

在加密秘密密钥的平行六边形中的刷新密文。

只需检查这一点能够解密到正确的值。我们如往常一样完成这一过程——对秘密钥（未经加密的）取模，然后对我们的明文域_I_取模。

完整的解密过程。

像时钟一样顺利，我们得到正确的值(1,3)！

魔法师！

但是，在整个过程中噪音发生了什么？

在这种情况下，噪音被表示为Bᵢ向量的最小线性组合，结果位于与密文相同的余因子中（在_J_中）。针对刷新后的密文，差异相对较小（只是我们基中的单个向量）。

找到原始_ψ₁+ψ₂_的代表并不那么简单。但是，在这里，我会展示余因子匹配的地方：

正好在那远处的黄色点上。鬼啊。

承认，这个误差增长与最初_J_的选择不当有关系。

在Gentry的构造中，秘密钥中的向量（R/J）是_IP_基向量的数十倍或数百倍大。我们的场景并未完全符合这些条件——因为我无法把所有那些点放在单个画面中！

但嘿，至少这个例子有助于说明_自引导_的过程是如何工作的。很大一部分噪音在有效地减少！

总结

当然，故事并未就此结束。目前来看，这个算法是非常_不实用_的。原始论文（以及！论文，这是更友好的阅读）实际上介绍了一些实用算法的改进，但我们不在这里讨论。

重要的是，这项工作证明了 FHE是可行的。这一代码已经被破解，看似不可实现的事情得以实现。

如今，新的、更闪亮的技术在Gentry原始工作上进行了改进（毕竟，这是15年前发表的）。例如，有这篇2011年的论文，提出了一个无需自引导的FHE的另一个方法；或者这篇2014年的论文，描述了一种更快速的FHE方法。

剧透：这篇文章没有比这里更简单的了！

这个领域已经演变了不少，所以我希望你能将这篇文章视为该主题的简短入门！

如果你需要在项目中实现FHE，有很多库可以使用。

结束语

这真是一段激动人心的旅程！

尽管在撰写这一系列文章的过程中我学习了很多，但我还是想说我在最开始就已经说过：我仍然不是该主题的专家——只是一个试图独自学习这项技能的人。

而且可能2023449326知识更多了一点！

不过，我认为这段旅程是极其丰富的。

如今可用的信息和工具的数量简直令人震惊。学习东西比以往任何时候都容易。

但有时，很难不陷入无休止的兔子洞，或者不被复杂的细节缠住——尤其是在处理高度专业化的主题时。我的目的是简化一点，使内容更易消化。

我真心希望这系列文章能帮助某人更好地理解加密技术提供的复杂概念。希望你在这个过程中也能笑一笑。至少对我来说，这一直都很有趣。

希望很快再见到你！并关注更多内容！

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～